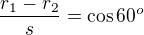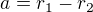Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 15. 01. 2011 19:39
Offline
#6 15. 01. 2011 21:09
Re: Komolý kužel
Povedal by som, ze tych 60° je prave Tvoja  .
.
Offline
#8 15. 01. 2011 22:21
Re: Komolý kužel
Děkuju za výpočty, ale mám ještě návrh, nešlo by poté udělat: a=r1-r2 ..přes Cos vypočítám, že a=3. Poté mi vyjde, že r1=r2+3. Dosadím do rovnice objemu:
21=r1^2+r1r2+r2^2 --> a všude, kde je r1 dosadím to r2+3.
vyjde mi: 0=r2^2+3r2-4, kořeny rovnice 1 a -4. r2=1 -->r1=4. Kořen rovnice r2=-4 nebudu uvažovat, jelikož to je záporné číslo. Je to správné řešení?
Offline