Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 09. 05. 2008 21:35
Re: Exponenciální rovnice
↑ halogan:
Mala rada co se tyce TeXu, pokud chces vyjadrit operaci nasobeni, tak pis radsi \cdot. Vypada to mnohem lip nez hvezdicka. Taky misto log pouzivej \log.
Ukazka:
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#8 10. 05. 2008 09:40 — Editoval didik (10. 05. 2008 09:48)
Re: Exponenciální rovnice
Je to podobný příklad jako ten, jehož řešení je popsáno výše.
Takže upravit na tvar: 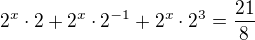
Zavést substituci: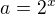
 Dále už jen stačí dopočítat a, vrátit se na substituci a spočíst x. To by už neměl být problém:-)
Dále už jen stačí dopočítat a, vrátit se na substituci a spočíst x. To by už neměl být problém:-)
EDIT: Koukám, že moje řešení je zbytečně složité.
Vím, že nic nevím.
Offline