Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nejmenší povrch rotačního válce (TOTO TÉMA JE VYŘEŠENÉ)
#2 10. 05. 2008 21:18
Re: Nejmenší povrch rotačního válce
↑ atn.hvc:
Zjisti si oba vzorce...pro objem i povrch rotacniho valce. V obou vzorcich se vyskytuji 2 promenne r (polomer podstavy) a v (na wikipedii znaci h) vyska valce. Ze vzorce pro objem V si vyjadri vysku valce v (h) a toto vyjadreni dosad do vztahu pro povrch. Tim dostanes rovnici pro povrch valce, kde se vyskytuje jen jedna promenna r a podle ni tento vztah derivujes a postupujes, jako pri hledani extremu. Pokus se o vypocet a kdyztak napis, pokud by ses nekde zasekl.
Offline
#3 10. 05. 2008 21:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nejmenší povrch rotačního válce
↑ atn.hvc:
tady se resilo neco podobneho: http://matematika.havrlant.net/forum/vi … hp?id=2155
Offline
#5 12. 05. 2008 22:11 — Editoval santic (12. 05. 2008 22:39)
Re: Nejmenší povrch rotačního válce
↑ atn.hvc:
Nemáš náhodou chybu v derivaci? Vychází mi totiž 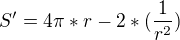
Poté postupuju takto: (omlouvám se, že to nepíšu v Texu)
DERIVACE
S' = 4*Pi*r - (2/r^2)
POSTAVÍM ROVNO 0
4*Pi*r - (2/r^^2) = 0 => r^3 = 2/(4*Pi) => r = 0,542 dm
DOSADÍM DO VZORCE PRO OBJEM
h = V/(Pi*r^2) => h = 1,084
DOSADÍM DO VZORCE PRO OBSAH
S = 2*Pi*r*(r+h) = 2*Pi*0,542*(0,542+1,084) = 5,537 dm^2
//Btw, zadání č. 17? :)
Offline
#6 12. 05. 2008 22:12 — Editoval jelena (12. 05. 2008 22:13)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nejmenší povrch rotačního válce
↑ atn.hvc:
vsechno se zda byt OK, pouze derivace ma byt 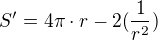 minus pred 2.
minus pred 2.
Ale jelikoz v dalsim vypoctu to nejak elegantne obchazis :-) , tak vysledek vychazi v poradku.
Editace :-) kolega byl rychlejsi :-)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nejmenší povrch rotačního válce (TOTO TÉMA JE VYŘEŠENÉ)

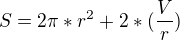
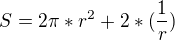

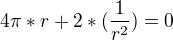
![kopírovat do textarea $r=\sqrt[3]{\frac{1}{2*\pi}}$](/mathtex/bd/bd40f6c82808a5fb807483fdaeda90e6.gif)