Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 01. 2011 18:55
říční přehrada tvaru lichoběžníka, díra ve dnu válcové nádoby
1. Jakou výslednou silou působí voda na říční přehradu tvaru lichoběžníka o základnách z_1=10m (dolní) a z_2=15m (horní) a výšce 5m. V jaké hloubce leží působiště výsledné síly?
Mohl by mi s tím prosím někdo pomoct? Počád se nemohu dobrat výsledku...
Výsledky:
F=1/3 ρghh(z_1 + z_2/2)
h_0= (3z_1 + z_2)h / 2(2z_1 + z_2)
2. Válcová nádoba je do výšky h= 70cm naplněna vodou. Plocha dna je 600cm2. Otvorem ve dně nádoby plochy 1cm2 voda vytéká. Za jakou dobu se nádoba vyprázdní do polovina a za jakou úplně?
Děkuju moc
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#2 20. 01. 2011 13:18
Re: říční přehrada tvaru lichoběžníka, díra ve dnu válcové nádoby
↑ Esperance:
1) Něco velmi podobného je tady. Jediný rozdíl je, že v odkazu je délka  konstantní a ty ji budeš muset vyjádřit jako funkci
konstantní a ty ji budeš muset vyjádřit jako funkci  .
.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 20. 01. 2011 13:45
Re: říční přehrada tvaru lichoběžníka, díra ve dnu válcové nádoby
↑ Esperance:
Podle rovnice kontinuity paltí  , kde
, kde 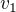 je rychlost klesání hladiny vody ve válci
je rychlost klesání hladiny vody ve válci  . Velikost výtokové rychlosti
. Velikost výtokové rychlosti 
 (- protože v_1 je orientovaná proti směru x)
(- protože v_1 je orientovaná proti směru x)
Po úpravě
Vypočítáš integrál, započítáš počáteční podmínky a je to
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 20. 01. 2011 18:04
Re: říční přehrada tvaru lichoběžníka, díra ve dnu válcové nádoby
děkuji, 2. příklad jsem tedy dopočítala:-) První byste mi, prosím, mohl někdo vysvětlit?
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#5 23. 01. 2011 00:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: říční přehrada tvaru lichoběžníka, díra ve dnu válcové nádoby
Zdravím,
dle doporučení kolegy Zdeňka v příspěvku 2 jsem vyjádřila úhel sklonu boční strany lichoběžníka od svislé polohy (od výšky např.). Je to tg(a)=2,5/5.
Potom L jako funkce x je  .
.
Je to v pořádku? Děkuji.
Offline
