Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » rovnica dotycnice ( tecny) ku krivke (TOTO TÉMA JE VYŘEŠENÉ)
#4 22. 01. 2011 20:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnica dotycnice ( tecny) ku krivke
↑ vysoka:
Zdravím,
máš implicitně zadanou funkci, v tom smyslu prosím pokračuj. A už by mohl nastat nějaký pokrok v technice matematického zápisu (když jž je to Tvůj 100. příspěvek - gratulace :-)
Offline
#7 22. 01. 2011 21:01
#8 22. 01. 2011 21:33
- Dana1
- Host
Re: rovnica dotycnice ( tecny) ku krivke
↑ vysoka:
y^2=2x+1 , dotyčnica y = kx + q obsahuje bod [-2;0]
Ak bod [-2;0] leží na priamke y = kx + q, musí platiť q = 2k, rovnica dotyčnice teda má tvar y = kx + 2k.
Pretože prienik dotyčnice a paraboly je jeden bod, po dosadení za y do rovnice paraboly musí mať vzniknutá kvadratická rovnica diskriminant rovný 0 (aby vyšiel jediný koreň).
Pre koeficient k dotyčnice mi po vyriešení vyšlo k1 = (odmocnina z 3)/3 (prvá dotyčnica) a k2 = - (odmocnina z 3)/3; Vieme, že q = 2k.
Ešte dosadiť do rovnice y = kx + q, vyjdú dve rovnice priamok - dotyčníc.
#11 23. 01. 2011 11:01 — Editoval Dana1 (23. 01. 2011 11:01)
- Dana1
- Host
Re: rovnica dotycnice ( tecny) ku krivke
↑ vysoka:
Áno, za y sa dosadí (kx + 2k). Dosadením hľadáme priesečník [x,y] dotyčnice a paraboly. Vyjde kvadratická rovnica pre x s parametrom k.
Pretože má existovať jediný priesečník paraboly a dotyčnice, vzniknutá kvadratická rovnica musí mať jediné riešenie. Takže hľadáme takú
hodnotu parametra k, ktorá spôsobí jediné riešenie tej kvadratickej rovnice. Túto hodnotu parametra zistíš z podmienky, že ak má byť 1 koreň,
diskriminant musí byť rovný 0.
Vyzerá to divoko, ale vyjde to pekne.
#12 23. 01. 2011 12:21
Re: rovnica dotycnice ( tecny) ku krivke
ok,
neviem ci tam mam chybu, ale:
dal som za Y ten vyraz kx+2k...
cize to je kx**2+4kx+4k**2
diskriminant je podla vzorca b**2-4ac=0
takze zavyrazy a, b, c som dosadil tie k - cka s konstantami ( cislami)
a tak vyslo 4k**2-16k**3=0
pred zatvorku sa da vynat 4k**2 a tak vyslo jedno k =0 a dalsie k = 1/4 ...
dakujem za pripadnu opravu ...:)
Offline
#14 23. 01. 2011 12:39
- Dana1
- Host
Re: rovnica dotycnice ( tecny) ku krivke
↑ vysoka:
(k^2)(x^2) + 4(k^2)x + 4(k^2) -2x -1 = 0
Diskriminant (4k^2 - 2)^2 - 4k^2(4k^2 -1), má byť rovný 0
#15 23. 01. 2011 13:31
Re: rovnica dotycnice ( tecny) ku krivke
ano bola tam chyba , vdaka, a ked dosadzam do diskriminantu ten "dlhy" clen , tak za cleny diskrimnantu beriem len cleny co su pri "x" ....
teda sa bralo za ax**2 + bx + c
a= k**2 , b = 4k**2 , alebo konstanta -2 ? vsak tam su dva cleny s "x" a za c = 4 alebo -1 ?
vdaka
Offline
#16 23. 01. 2011 14:55 — Editoval Dana1 (23. 01. 2011 15:15)
- Dana1
- Host
Re: rovnica dotycnice ( tecny) ku krivke
↑ vysoka:
Ten diskriminant som vypísala, x musíš z tých dvoch výrazov VYŇAŤ, potom b je tá zátvorka pred x, teda +(4k^2 - 2).
Výrazy s x sú: 4(k^2)x a -2x ... vyjmeš x a dostaneš zátvorku ako v predchádzajúcom riadku. To je člen pri x v kvadratickej rovnici.
#17 25. 01. 2011 10:40
Re: rovnica dotycnice ( tecny) ku krivke
ok, bol pochopitelnyl ten diskriminant a, b, c vľak to nebolo az take tazke ... :)
teraz sa to roznasobi a tak vyslo -4k**2+4=0 , a vsak tak mi vyslo k**2 = 1 ... nebolo to treba vycislovat a radsej dosadit do tej y= kx++q ?
vdaka
Offline
#18 25. 01. 2011 11:16 — Editoval Dana1 (25. 01. 2011 11:22)
- Dana1
- Host
Re: rovnica dotycnice ( tecny) ku krivke
↑ vysoka:
y^2 = 2x + 1, dotyčnica y = kx + q ........ lebo (-2;0) leží na dotyčnici, q = 2k a dotyčnica má rovnicu y = kx + 2k
(kx + 2k)^2 = 2x + 1
(k^2) *( x^2) + 4 k^2 x + 4k^2 -2x -1 = 0, neznáma je x
(k^2) *( x^2) + 4 k^2 x -2x + 4k^2-1 = 0
(k^2) *( x^2)+ (4 k^2-2)x + (4k^2-1) = 0, a = (k^2) b = (4 k^2-2) c = (4k^2-1)
diskriminant má byť 0, takže
(4 k^2-2)^2 - 4 (k^2) (4k^2-1) = 0
16k^4 - 16k^2 +4 -16k^4 + 4 k^2 = 0
4 = 12 k^2
1/3 = k^2
k = +-(odmocnina z 3)/3
#19 25. 01. 2011 11:21 — Editoval Cheop (25. 01. 2011 11:31)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: rovnica dotycnice ( tecny) ku krivke
↑ vysoka:
Rovnice tečny bude  - prochází bodem (-2,0) - dosadíme do předpisu souřadnice bodu tj:
- prochází bodem (-2,0) - dosadíme do předpisu souřadnice bodu tj: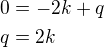
Rovnice tečny bude: 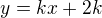 - toto dosadíme do rovnice paraboly a určíme k tak, aby přímka měla s parabolou 1 společný bod.
- toto dosadíme do rovnice paraboly a určíme k tak, aby přímka měla s parabolou 1 společný bod.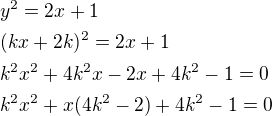 toto je kvadr. rovnice, aby to byla tečna pak diskriminant této rovnice =0 tj:
toto je kvadr. rovnice, aby to byla tečna pak diskriminant této rovnice =0 tj: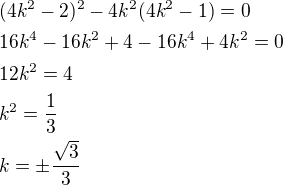 - dosadíme do předpisu tečny:
- dosadíme do předpisu tečny:
pro 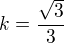
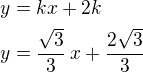
Pro 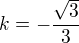
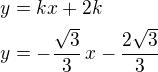
Řešení: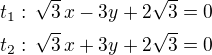
Obrázek:
Nikdo není dokonalý
Offline
#22 25. 01. 2011 12:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnica dotycnice ( tecny) ku krivke
Zdravím vás,
ještě kolegovi doplním postup přes derivaci implicitní funkce: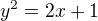 derivace:
derivace: 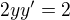 , odsud
, odsud 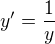
rovnice tecny 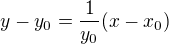 (1)
(1)
Souřadnice body dotyku nemáme, pouze máme jiný bod, který je na přímce, ale není na parabole, do rovnice primky dosazujeme souradnice takto: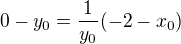 ,
,
odsud 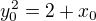 , dosazujeme do rovnice paraboly a najdeme souradnice bodu dotyku.
, dosazujeme do rovnice paraboly a najdeme souradnice bodu dotyku.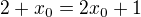
Po dopočtu hodnot y_0 dosadíme do (1)
Jediný a právý důvod tohoto příspěvku - připomenout kolegovi vysoka, aby označil ještě některé svá témata za vyřešená. Děkuji.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » rovnica dotycnice ( tecny) ku krivke (TOTO TÉMA JE VYŘEŠENÉ)