Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 01. 2011 19:05 — Editoval Esperance (21. 01. 2011 19:08)
fyzické kyvadlo, střela
1.-Jakou rychlostí musí narazit střela hmotnosti m kolmo na spodní konec svisle zavěšené tyče hmotnosti M a délky l, aby ji vychýlila o úhel 90° ? Střela v tyči uvízne.
2. Tenká homogení tyč hmotnosti M a délky l se kývá kolem osy, která je k ní kolmá a prochází jejím horním koncem. a) určete periodu malých kyvů b) existuje na tyči místo do kterého můžeme připevnit těleso malých rozměrů o značné hmotnosti, aby se doba kyvu nezměnila? Kde?
ad1) v= [ (gl (M+2m) (M/3 + m) )^1/2]/m ... nevím, co dělám špatně, nedokážu se dobrat tohoto výsledku
ad2) T= 2pi (2l/3g)^1/2 .... tady mi zase vychází jiný koeficient než 2/3
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
- (téma jako vyřešené označil(a) Esperance)
#2 22. 01. 2011 15:56
Re: fyzické kyvadlo, střela
↑ Esperance:
1. toto je prakticky stejné
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 22. 01. 2011 16:38
Re: fyzické kyvadlo, střela
↑ Esperance:
2a)
moment setrvačnosti tyče vzhledem k těžišti 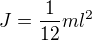
perioda fyz. kyvadla 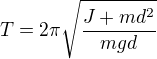 , kde
, kde  je vzdálenost osy od těžiště
je vzdálenost osy od těžiště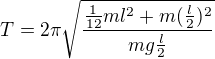
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 23. 01. 2011 15:29
Re: fyzické kyvadlo, střela
za 2 děkuji. Vím, že je to podobné, ten předchozí (pravděpodobně jedeme s uživatelem ze stejných skript) jsem spočítala v pořádku. Na tento nemohu přijít...
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#5 23. 01. 2011 16:37
Re: fyzické kyvadlo, střela
↑ Esperance:
při srážce ZZ momentu hybnosti 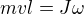
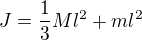

potom ZZE 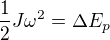
 těžiště tyče se zvedne o
těžiště tyče se zvedne o  , střela se zvedne o
, střela se zvedne o 
zbytek je hokej s písmenkama
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 23. 01. 2011 18:08
Re: fyzické kyvadlo, střela
můj problém tedy spočíval akorát na začátku http://www.matweb.cz/cgi-bin/mimetex.cg … 3Ml^2+ml^2 .. v 1/3... dávala jsem
1/12 Ml^2 - jako moment tyče.. proč je tam 1/3? Díky
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#7 23. 01. 2011 18:49
Re: fyzické kyvadlo, střela
↑ Esperance:
Protože 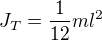 je moment setrvačnosti vzhledem k těžišti. ALe ta tyč se otáčí kolem osy procházející krajním bodem.
je moment setrvačnosti vzhledem k těžišti. ALe ta tyč se otáčí kolem osy procházející krajním bodem.
Podle Steinerovy věty 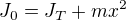 , kde
, kde  je vzdálenost těžiště - osa, tj.
je vzdálenost těžiště - osa, tj. 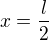
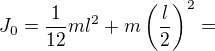
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
