Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Slovní úlohy asi na extrémy (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 05. 2008 16:08
Slovní úlohy asi na extrémy
Zdravím, dneska mě dostihla nepotěšující zpráva, že jsme dostali ve škole dalších pár příkladů. Všechny jsem jakž takž dal, ale slovní úlohy nevim co s tím. Jelikož to byla série příkladů na extrémy, tak bych řekl, že se to bude ubírat touto cestou, ale opravdu mě nenapadá co a jak..:-(
1. Mezi všemi rotačními válci s povrchem S=600pi cm^2 najděte ten, který má největší objem.
2. Mezi všemi rovnoramennými trojúhelníky daného obvodu 2s vyberte ten, jehož rotací
kolem jeho osy vznikne těleso nejvìtšího objemu.
Offline
#2 12. 05. 2008 16:14
Re: Slovní úlohy asi na extrémy
No hned jak jsem to odeslal, tak mi svitlo a možná jsem vyřešil jeničku
Kdyby někoho zajímalo, tak zde je moje(snad dobré) řešení:

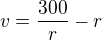

 ... zde hledám glob.maximum fce
... zde hledám glob.maximum fce na
na 
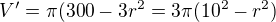

V 10 je lokální maximum 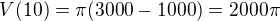
Hledaný válec má rozměry: 
a výška 
Ale tu dvojku mi nějak nejde ani teď.... Díky předem za pomoc:-)
Offline
#3 12. 05. 2008 16:48
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
↑ NetFenix:
Zdravim :-)
zkus zadani ve dvojce vzit jako "nalezeni nejvetsiho objemu kuzelu, v jehoz rezu je zadany rovnoramenny trojuhelnik". Rotaci rovnoramenneho trojuhelniku kolem vlastni osy vznika kuzel. OK?
Offline
#5 12. 05. 2008 18:40
Re: Slovní úlohy asi na extrémy
No vůbec mi to nejde, furt mi tam skáčou minimálně dvě proměnné.
Si vyjádřím jako by ten trojuhelnik, kdy základna je d(průměr) a tedy d/2=poloměr r; no a zbylé dvě stěny pak při rotaci vytvoří pláš?, když ale si chci vyjádřit výšku kužele, tak mi to nějak nejde (nebo spíše jde ale ne tak jak potřebuju), nemohl by mi s tím někdo prosím píchnout? Díky
Offline
#6 12. 05. 2008 22:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
↑ NetFenix:
Obvod trojuhelniku 2s se sklada z podstavy = prumeru (d=2r) a dvou stejnych ramen (b),
tedy delka ramena b=(2s -2r)/2 = s-r
vysku trojuhelniku (je to take vyska kuzele) vypoctes pomoci Pythagorovy vety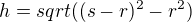
Objem mame vyjadren jako funkci r : trochu upravis vyraz pod odmocninou, derivujes (s se povazuje za konstantu) a melo by to byt, doufam :-).
trochu upravis vyraz pod odmocninou, derivujes (s se povazuje za konstantu) a melo by to byt, doufam :-).
OK?
Offline
#8 13. 05. 2008 14:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
↑ NetFenix:
derivace s bude 0, derivace s^2 bude take 0, ale derivace treba 2s*r (r mame za promennou) bude 2s. To jen pro poradek, urcite to vis :-)
Offline
#10 13. 05. 2008 17:31 — Editoval jelena (13. 05. 2008 17:31)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
↑ NetFenix:
trochu opravim - myslim, ze ma byt minus pred (2s) v druhem zlomku, ale to je detail
 - doufam, ze jsem to vypocetla dobre :-)
- doufam, ze jsem to vypocetla dobre :-)
zbyva uz vyresit, kdy tento vyraz se rovna 0, jmenovatel zatim ponechame, v citateli s, r nemuze byt 0 ze zadani, zustava
2s-5r = 0,
r=0,4s (tedy pokud r bude 2/5 obvodu trojuhelniku). Je potreba zkontrolovat, zda pri tomto vysledku v jmenovateli neni nula (pro poradek) OK?
Offline
#11 13. 05. 2008 17:43
Re: Slovní úlohy asi na extrémy
jéje já se omlouvám, ale moc to nechápu, abych řekl pravdu. Pokud dostanu fci, vím co dělat, ale jak to mám aplikovat na úlohu je to bohužel pro mě, jak se zdá jakýsi problém.
To znamená, že poloměr toho největšího kuželu je 0,4s a tedy základna trojúhelníku je 2*0.4s a pak tedy ramena jsou 0.6s a 0.6s. Myslím si to správně?
Jo a hledám pravděpodobně nikoliv lokální extrém, ale asi globální, je třeba dokazovat, že právě toto je globálním extrémem?
Offline
#12 13. 05. 2008 20:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
↑ NetFenix:
Polomery podstavy a ramena mas vypoctena dobre.
Dokazat, ze je to extrem muzeme pomoci zmeny znamenka prvni derivace - myslim, ze by to slo po dosazeni za r treba 0,2s (coz je hodnota pred 0,4s) a za r dat 0,6 s (coz je po 0,4 s). V prvnim pripade mame kladny vysledek, v druhem zaporny, cimz dokazeme, ze v 0,4 s nastava maximum
OK?
Offline
#13 27. 04. 2009 21:45
- zbynek.maier
- Zelenáč
- Příspěvky: 7
- Reputace: 0
Re: Slovní úlohy asi na extrémy
Prosim Vas, nemate nekdo ten priklad s tema trojuhelnikama rovnoramennyma jeste nekde na papire vypocten? hodne by mi to pomohlo, ptz sem se do toho zamotal
Offline
#14 28. 04. 2009 17:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
↑ zbynek.maier:
Jelikož kolega využil jiných komunikačních kanalů a ja zrovna mám splněny jiný daleko složitější úkol a ...., tak vytvořím takový souhrn předchozích příspěvků:
Zadání: Mezi všemi rovnoramennými trojúhelníky daného obvodu 2s vyberte ten, jehož rotací
kolem jeho osy vznikne těleso největšího objemu.
Rotaci trojuhelníku kolem jeho osy vznika kužel:
http://forum.matweb.cz/upload/273-zbynek.JPG
výška kuželu: 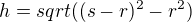
Objem kuželu:
Objem kuželu je funkce proměnné r: 

Pro nalezení extrému funkce potřebujeme najit 1. derivaci: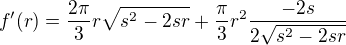

V bode podezřelém z extrému 1.derivace se rovná 0.
V citateli s, r nemuze byt 0 ze zadani, zustava, že 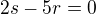 ,
,
(pokud r bude 2/5 obvodu trojuhelniku).
Je potreba zkontrolovat, zda pri tomto vysledku v jmenovateli neni nula (pro poradek)
Ověřit, že v bodě r=0.4s nastává maximum funkce můžeme pomoci zmeny znamenka prvni derivace - po dosazeni za r 0,2s (coz je hodnota pred 0,4s) a za r dat 0,45 s (coz je po 0,4 s). V prvnim pripade mame kladny vysledek, v druhem zaporny, cimz dokazeme, ze v 0,4 s nastava maximum.
Škoda, že neposlouchám rozhlas ani nesleduji televizi, nechala bych si alespoň zahrat...
Už OK?
Offline
#15 28. 04. 2009 20:48
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Slovní úlohy asi na extrémy
↑ jelena:
Preji pekny den, videl jsem dlouhy prispevek, tak jsem se zacetl, jestli nahodou neuvidime reseni pomoci smesi - ze by se to pridalo k legendarnimu prispevku #38 ve vlakne http://forum.matweb.cz/viewtopic.php?id=55&p=2 a mnoha dalsim, napr. #7 v http://forum.matweb.cz/viewtopic.php?id=2317 , ke kterym se obcas vracim.
Perfektni shrnuti, ted uz tomu asi bude rozumet kazdy, tak se to pokusim opet trosku zamlzit :) Ja bych jenom pro urychleni (kdyz ma treba clovek moc prace a musi fungovat) polozil bez ujmy na obecnosti s=1 (vysledek potom zvetsim s-krat, objemy se zvetsi s^3 -krat), maximalizoval bych V^2 a vynechal multiplikativni konstanty. Takze by se pocital lokalni extrem funkce  , potom
, potom  a
a 
-------------------------------------
Tak ty máš moc práce?“
„Moc, pane řídící, já musím pořád fungovat.“
Offline
#16 28. 04. 2009 23:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
↑ kaja(z_hajovny):
Neměla jsem ještě přiležitost zareagovat na transformační proces a abych pravdu řekla, nevím, co ukládá etiketa v podobných situacich - předpokládám ovšem, že pěkný pozdrav určitě bude na místě :-)
Předpřechozí příspěvek vznikl pochopitelně poctivým kopírováním dílů z před-před-před-předchozích příspěvků. Originalita spočívá v přidání 2 skladeb a v opravě dosazování - místo 0,6s (což není dobře :-) je 0,45s.
Zamlžení rozumím, zda tomu rozumí i kolegové od informatiků, to neposoudím.
Jinak tato úloha patří tak na kontrolní desetiminutovku, nebo já nerozumím smylu slova "Projekt".
K slovesu "musím" - to používá okolí, já "nemusím".
A jelikož se zatím nechytám, který díl čteme, tak k problematice "musím" budu citovat kartičku od našeho syna, na kterou z nařízení tatínka napsal: "nebudu maminku otravovat (provokovat) hloupími řečmi" - to je originál znění.
Zdravím Vás :-)
Offline
#17 10. 05. 2009 13:11
Re: Slovní úlohy asi na extrémy
Zdravím tento topic!
Vím že "nebudu maminku otravovat (provokovat) hloupími řečmi", ale i přesto si se vší pokorou dovolím, pač mi pár hloupých věcí není jasných.. hehe
Tedy:
----->
S čeho plyne při hledání toho extrému že: V citateli s, r nemuze byt 0 ze zadani, zustava že 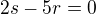 ... jaktože nemusíme počítat celou f'(r) = 0 ??
... jaktože nemusíme počítat celou f'(r) = 0 ??
----->
Je potreba zkontrolovat, zda pri tomto vysledku v jmenovateli neni nula (pro poradek) .. stačí to udělat tak, že si za s dosadím 1, r tedy bude 0.4 a proste si tu funkci vypoctu a skontroluju jestli není ve jmenovateli 0 ?
----->
Mno a ... proč při ověřování extrému volíme zrovna body 0.2 a 0.45 ?? Proč je například 0.6 špatně?
Offline
#18 10. 05. 2009 13:43 — Editoval jelena (10. 05. 2009 14:20)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
↑ Grimbor:
Zdravím, maminky se provokuji úplně jinými řečmi, než otázky na extrémy funkce (například otázkou "Proč to mám dělat, když nikdo jiný to nemusí?" Odpověď maminky: "Protože jsem to řekla" a je potřeba mít za sebou silnou autoritu tatinka)
Tak teď se to pokusím zvládnout bez silné autority.
----->
S čeho plyne při hledání toho extrému že: "V citateli s, r nemuze byt 0 ze zadani, zustava že 2s-5r = 0 ... jaktože nemusíme počítat celou f'(r) = 0 ??"
Samozřejmě můžeme, ale již na začátku úlohy si musíme stanovit podmínky pro řešení - žádný rozměr trojuhelníku nemůže být nulový ani záporný, další podmínka by měla být, že nalezené rozměry budou splňovat trojuhelníkovou nerovnost (součet 2 stran je větší, než třetí strana). Proto jsem uvedla tuto poznámku, že "ze zadání"
----->
Je potreba zkontrolovat, zda pri tomto vysledku v jmenovateli neni nula (pro poradek) .. stačí to udělat tak, že si za s dosadím 1, r tedy bude 0.4 a proste si tu funkci vypoctu a zkontroluju jestli není ve jmenovateli 0 ?
Do výrazu 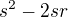 dosadím r=0,4s a zkontroluji, že výsledek není 0.
dosadím r=0,4s a zkontroluji, že výsledek není 0. 
Úplně korektní by bylo určit definiční obor pro funkci "Objem" a pro 1. derivaci teto funkce podmínka pro určení def oboru by byla taková:  (zde už mám zahrnutou i derivaci, jen pro objem by to bylo "větší nebo se rovná"
(zde už mám zahrnutou i derivaci, jen pro objem by to bylo "větší nebo se rovná" 
 , s musí být kladné, proto
, s musí být kladné, proto 


----->
Mno a ... proč při ověřování extrému volíme zrovna body 0.2 a 0.45 ?? Proč je například 0.6 špatně?
Dosazujeme body před 0,4s (tam můžeme cokoliv v intervalu (0, 4s). Body po 0,4s musí splňovat definiční obor, který jsme stanovili v předchozím kroku (r mělo být menší než 0,5s). Proto můj první návrh nebyl OK a proto jsem ho opravila na 0,45s.
OK?
--------
Nejsou hloupé otázky, ale občas jsou hloupé odpovědí (tak pokud ta moje zrovna splňuje tuto definici, tak se určitě najde někdo z kolegů, kdo mi rychle srovná myšlenky, již teď děkuji). Pravda, jsou situace, kdy odpověď "Protože jsem řekla" je jedina vhodná.
Upřímně řečeno, mé povědomí o kvalitě ostravských informatiku se velmi vylepšuje pozitivním směrem, děkuji, kolego ↑ Grimbor:
Editace: opravila jsem dosazování do jmenovatele.
Offline
#19 10. 05. 2009 15:12
Re: Slovní úlohy asi na extrémy
Už se mi to jeví pochopitelnější, avšak stále mi není jasná ta věc s dokazováním, že jmenovatel bude nenulový.. co s tím má vlastně společného ten definiční obor... respektivě, jak to pomoci něho dokážu..
Ja bych třeba pro dokázání nenulovost čitatele udělal následovné:
Avšak je mi jasné že ten definiční obor si stejně budu muset určit, abych pak mohl dokázat že se jedná o o.l.maximum dané funkce ... který musím vlastně znát, i kdybych se rozhodl dokazovat extrém přes monotoonii nebo přes konvex/konkav ...
Offline
#20 10. 05. 2009 15:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
↑ Grimbor:
Definiční obor pro funkci "objem" je proto, že v zápisu funkce V je odmocnina (výraz pod odmocninou musí být nezáporný).
Navíc úloha je určitým způsobém formulována, což nás už od zadání omezuje (myslím, že pokud omezení popišeš na začátek, bude to jasné). K tomu přidaš definiční obor vytvořené funkce pro V. A pokud v průběhu výpočtu provádíme různé úpravy, musí být povoleny.
Výsledek výpočtu (0,4 s) můžeš překontrolovat tak, jak jsi udělal (nenulovost jmenovatele 1. derivace a nezápornost výrazu pod odmocninou bude potvrzena).
Extrém můžeš dokazovat přes druhou derivaci, ale podle mého je to zbytečný krok navíc. Změna znaménka před a po bodu podezřelém z extrému je dostačující.
OK?
Offline
#21 10. 05. 2009 18:49 — Editoval Grimbor (10. 05. 2009 18:51)
Re: Slovní úlohy asi na extrémy
Nu, nějak jsem si to tedy sesumíroval a snad i pochopil, i když tedy od takových těch osvícených stavů, kdy se mi před očima zjevují celé průběhy funkcí a kdy na nich názorně vidím kde leží jaky bod či prusečík, jsem u tohoto příkladu ještě hodně daleko..ale to se možna poddá..hehe
Já vúbec, mám strašný zlozvyk přehlížet jakési základní poznatky a potom si uvažování zbytečně komplikovat ... zvláš´t tedy v matematice... viz. třeba to, proč ze zadání víme že r a s se nebudou rovnat nule ... a přitom je to tak do očí bijící záležitost že přece nemuže být trojuhelník s nulovou podstavou :o)
Každopídně.. ještě bych se chtěl zeptat, když tak koukám na to zadání, vlastně nevím co po mě v tom příkladu chcou ... vyberte největší trojuhelník...a teď..zdali bude stačit tvrzení, pro největší vybraný trojuhleník bude platit že: r = 0.4s
Anebo nějak sformulovat další vzorce.. třeba že o = 2b + 0.8s (jestli to tak může být) ...či jiné...
Offline
#22 10. 05. 2009 19:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
Grimbor napsal(a):
když tak koukám na to zadání, vlastně nevím co po mě v tom příkladu chcou
To je dobrý přístup - na závěr úlohy se zeptat - a co to chtěji.
Ale dobře - ta tvoje úvaha na závěr je v pořádku:
je hodně různých rovnoramenných trojuhelníku s obvodem 2s a je potřeba vybrat ten, kterym, když budeme točit kolem osy, tak vyrobíme největší rotáční kužel.
A správně vybereš ten, který má základnu 2*0,4s (2* je proto, že jsme celou dobu počítali pouze r - poloměr podstavy kuzelu).
Tedy trojuhelník, který splňuje podmínky: obvod (zadáno) = 2s, základna trojuhelníku 0,8s, ramena trojuhelníku (2s - 0,8s)/2 = 0,6s
OK?
Offline
#24 11. 05. 2009 00:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy asi na extrémy
↑ JOnas:
Tak jsem něco zabrnkala v původním tématu, tak tam pokračuj - není nutné psat do více témat stejné zadání.
Hodně zdaru.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Slovní úlohy asi na extrémy (TOTO TÉMA JE VYŘEŠENÉ)