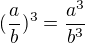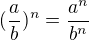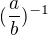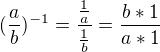Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 27. 01. 2011 19:24
Re: umocňování zlomků
Všeobecne platí: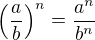
no vidíš tam nejakú analógiu ?
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#5 27. 01. 2011 19:35 — Editoval mikl3 (27. 01. 2011 20:08)
Re: umocňování zlomků
↑ hradecek: no zas tak všeobecně platí :)
platí to pro 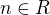 (bez urážky)
(bez urážky)
ano nedává to smysl, protože to je editované
Offline
#10 27. 01. 2011 19:51 — Editoval hradecek (27. 01. 2011 19:52)
Re: umocňování zlomků
↑ mikl3: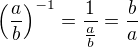
píšeš("tvrdíš") dve rôzne veci zároveň...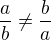
ale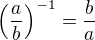
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#11 27. 01. 2011 19:53 — Editoval mikl3 (27. 01. 2011 19:54)
Re: umocňování zlomků
↑ hradecek: tím myslíš konkrétně co? já se ptám, zda platí 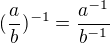
tohle 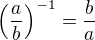 platí, to vím
platí, to vím
Offline
#12 27. 01. 2011 19:55 — Editoval hradecek (27. 01. 2011 19:57)
Re: umocňování zlomků
↑ mikl3:
a ja kopírujem to isté čo povedal ↑ BakyX: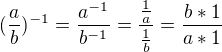
tak určite vieš že platí aj 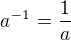
a písmenko si tam môžeš dať hociaké a aj tak to bude platiť, kľudne aj 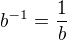
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#13 27. 01. 2011 20:02 — Editoval mikl3 (27. 01. 2011 20:03)
Re: umocňování zlomků
↑ hradecek: bez toho vtípku prosím, já zde nechci nikoho shazovat, nýbrž si ověřit, prodiskutovat mé matematické závěry
Offline
#14 27. 01. 2011 20:06 — Editoval hradecek (27. 01. 2011 20:15)
Re: umocňování zlomků
↑ mikl3:
OT:
Ak som ťa urazil, tak sa ti ospravedlňujem :), koniec koncov, mýlime sa všetci :).
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#15 27. 01. 2011 20:07
Re: umocňování zlomků
↑ hradecek: přesně tak, děkuji za omluvu (nesmíte si to brát špatně (plurál), já jsem "malá ryba", ale hodně mě toho zajímá a i občas se stane něco podobného :D)
Offline
#16 27. 01. 2011 20:15
Re: umocňování zlomků
↑ mikl3:
OT:
Kľudne aj singulár ;-), lebo tiež nie som "najväčšia ryba" :))).
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#17 27. 01. 2011 20:19
Re: umocňování zlomků
↑ hradecek: já jsem si to myslel v hlavě, pak jsem koukl do tabulek, tak to taky stálo (jenže u jiné úpravy :D), pak se to tady nějak začínalo bortit (mé postupy) a byl jsem přesvědčen (dneska malinko proti vůli, tak jsem to chvíli odmítal), že to tak není, nyní vím o poznatek více a děkuji, konec OT
Offline
#18 27. 01. 2011 21:51
Re: umocňování zlomků
↑ hradecek:
Btw..Spisovne je
"pokojne" a nie "kľudne".."pokoj" a nie "kľud"..Kľud sme my Slováci prebrali od bratov Čechov :)
1^6 - 2^6 + 3^6 = 666
Offline