Matematické Fórum

kety · 21. 01. 2011 14:53

[IMG]http://www.sdilej.eu/pics/19ec6d0dc2ce745c0e54d38bdef72903.bmp" alt="<a href="http://www.sdilej.eu/#19ec6d0dc2ce745c0e54d38bdef72903.bmp">[IMG]http://www.sdilej.eu/pics/19ec6d0dc2ce745c0e54d38bdef72903.bmp" />[/img]vubec si s timto prikladem nevim rady nevite nekdo prosim jak to dokazat?

Pavel · 21. 01. 2011 15:44

↑ kety:

a nemá být $\{a_k\}$ posloupnost přirozených čísel?

petrkovar · 21. 01. 2011 15:56

Nemyslím, že 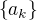$\{a_k\}$ má být posloupnost přirozených čísel, neboť součet má být libovolné (tedy i záporné) racionální číslo.
Vlákno dostalo do nadpisu "matematickou indukci". Má se opravdu dokazovat matematickou indukcí, nebo jsou doboleny i jiné přístupy?

Pavel · 21. 01. 2011 16:07

↑ petrkovar:

To jsem přehlédl. Nicméně dá se myslím dokázat, že libovolné kladné racionální číslo lze zapsat jako konečnou sumu převrácených hodnot různých přirozených čísel. Pak by to rozšíření na záporná racionální čísla bylo triviální. Stačilo by pracovat s konečnou sumou převrácených hodnot záporných celých čísel.

Kdyby se totiž daná úloha dokazovala pro kladná racionální čísla (za použití sumy převr. hodnot přirozených čísel), tak v tom důkazu "mlhavě" vidím použití tzv. "metody nekonečného sestupu".

Detaily bych musel promyslet.

petrkovar · 21. 01. 2011 17:00

Předpokládejme nejprve, že $q>0$ .
Využil bych, že harmonická řada diverguje: $\sum_{i=1}^{\infty}\frac{1}{i}\to\infty$ . Označme $n$ první takový index, že $\sum_{i=1}^{n}\frac{1}{i}>q$ .
A nyní se podíveme na tři možnosti, zda rozdíl $q-\sum_{i=1}^{n-1}\frac{1}{i}$ (pozor na $n-1$ ) je více, stejně nebo méně než $\frac{1}{n}$ .

Potom separátně vyřešíme $q=0$ a $q<0$ .

kety · 21. 01. 2011 18:29

↑ petrkovar:
muzeme pouzit i jiny postup

kety · 21. 01. 2011 18:33

↑ Pavel:
mohl by si prosim k tomuhle postupu napsat neco jeste trochu blizsiho prijde mi to nejschudnejsi reseni

Pavel · 22. 01. 2011 22:01

↑ kety:

Ukažme, že každé kladné racionální číslo lze zapsat jako konečnou sumu převrácených hodnot různých přirozených čísel.

Nechť tedy 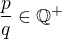$\frac pq\in\mathbb{Q}^+$ . Pak zkonstruujme rostoucí posloupnost $\{a_n\}_{n=1}^i$ přirozených čísel takových, že

$\Large\frac pq=\sum_{n=1}^i\frac 1{a_n}\,.$

Začněme myšlenkou, kterou tady představil ↑ petrkovar:.

1. Označme $k$ takový index, že $\Large\sum_{n=1}^{k}\frac{1}{n}\leq\frac pq$ a zároveň $\Large\sum_{n=1}^{k+1}\frac{1}{n}>\frac pq$ .

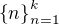a) Jestliže v neostré nerovnosti nastane rovnost, pak $\Large\sum_{n=1}^{k}\frac{1}{n}=\frac pq$ a hledaná posloupnost je ve tvaru $\{n\}_{n=1}^k$ . Úloha je vyřešena.

b) Nechť tomu tak není, tzn. $\Large\sum_{n=1}^{k}\frac{1}{n}<\frac pq<\sum_{n=1}^{k+1}\frac{1}{n}$ .

2. Definujme racionální číslo 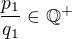$\frac{p_1}{q_1}\in\mathbb{Q}^+$ takto:

$\Large\frac{p_1}{q_1}:=\frac pq-\sum_{n=1}^{k}\frac{1}{n}.$

Pak z definice a z obou výše uvedených nerovností platí, že

$\Large 0<\frac{p_1}{q_1}<\frac {1}{k+1}\,.$

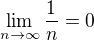Protože $\lim_{n\to\infty}\frac 1n=0$ , pak můžeme najít takové přirozené číslo $k_1>k$ , že $\Large \frac 1{k_1+1}\leq\frac{p_1}{q_1}<\frac{1}{k_1}$ .

a) Jestliže nastane v neostré nerovnosti rovnosti, tzn. $\Large \frac 1{k_1+1}=\frac{p_1}{q_1}$ , pak

$\Large \frac pq=\sum_{n=1}^{k}\frac{1}{n}+\frac{p_1}{q_1}=\sum_{n=1}^{k}\frac{1}{n}+\frac{1}{k_1+1}$ a hledaná posloupnost je ve tvaru $1,2,\,\ldots\,,k,k_1+1$ . Úloha je vyřešena.

b) Nechť tomu tak není, tzn. $\Large \frac 1{k_1+1}<\frac{p_1}{q_1}<\frac{1}{k_1}$ .

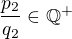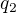3. Definujme racionální číslo $\frac{p_2}{q_2}\in\mathbb{Q}^+$ tak, že $p_2$ resp. $q_2$ je čitatel resp. jmenovatel zlomku 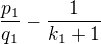$\frac {p_1}{q_1}-\frac 1{k_1+1}$ v nezkráceném tvaru, tj.

$\Large \frac {p_1}{q_1}-\frac 1{k_1+1}=\frac{\overbrace{p_1(k_1+1)-q_1}^{p_2}}{\underbrace{q_1(k_1+1)}_{q_2}}\,.$

Z analogických důvodů jako v předchozím bodu můžeme najít takové přirozené číslo $k_2>k_1$ , že $\Large \frac 1{k_2+1}\leq\frac{p_2}{q_2}<\frac{1}{k_2}$ .

a) Jestliže nastane v neostré nerovnosti rovnosti, tzn. 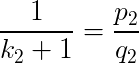$\Large \frac 1{k_2+1}=\frac{p_2}{q_2}$ , pak

$\Large \frac pq=\sum_{n=1}^{k}\frac{1}{n}+\frac{p_1}{q_1}=\sum_{n=1}^{k}\frac{1}{n}+\frac{p_2}{q_2}+\frac{1}{k_1+1}=\sum_{n=1}^{k}\frac{1}{n}+\frac{1}{k_1+1}+\frac{1}{k_2+1}$ a hledaná posloupnost je ve tvaru $1,2,\,\ldots\,,k,k_1+1,k_2+1$ . Úloha je vyřešena.

b) Nechť tomu tak není, tzn. $\Large \frac 1{k_2+1}<\frac{p_2}{q_2}<\frac{1}{k_2}$ .

4. Definujme racionální číslo 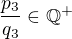$\frac{p_3}{q_3}\in\mathbb{Q}^+$ tak, že 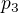$p_3$ resp. $q_3$ je čitatel resp. jmenovatel zlomku $\frac {p_2}{q_2}-\frac 1{k_2+1}$ v nezkráceném tvaru, tj.

$\Large \frac {p_2}{q_2}-\frac 1{k_2+1}=\frac{\overbrace{p_2(k_2+1)-q_2}^{p_3}}{\underbrace{q_2(k_2+1)}_{q_3}}\,.$

Pak můžeme najít takové přirozené číslo $k_3>k_2$ , že $\Large \frac 1{k_3+1}\leq\frac{p_3}{q_3}<\frac{1}{k_3}$ .

a) Jestliže nastane v neostré nerovnosti rovnosti, tzn. 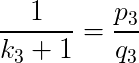$\Large \frac 1{k_3+1}=\frac{p_3}{q_3}$ , pak

$\Large \frac pq=\sum_{n=1}^{k}\frac{1}{n}+\frac{p_1}{q_1}=\dots=\sum_{n=1}^{k}\frac{1}{n}+\frac{1}{k_1+1}+\frac{1}{k_2+1}+\frac{1}{k_3+1}$ a hledaná posloupnost je ve tvaru $1,2,\,\ldots\,,k,k_1+1,k_2+1,k_3+1$ . Úloha je vyřešena.

b) Nechť tomu tak není, tzn. $\Large \frac 1{k_3+1}<\frac{p_3}{q_3}<\frac{1}{k_3}$ .

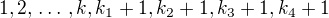5. Pak můžeme pokračovat dál a konstruovat racionální čísla $\frac{p_4}{q_4}$ atd. resp. posloupnosti $1,2,\,\ldots\,,k,k_1+1,k_2+1,k_3+1,k_4+1$ atd.

Zbytek nechám na Tobě:

Nyní stačí ukázat, že celý postup skončí po konečně mnoha krocích. Ukaž, že posloupnost čitatelů 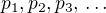$p_1,p_2,p_3,\,\ldots$ je klesající posloupnost přirozených čísel. To nutně implikuje, že pro dostatečně velký index musí být členy této posloupnosti nulové, což ukončuje výše popsanou proceduru a dokazuje to, že ke každému kladnému racionálnímu číslu exituje konečná posloupnost přirozených čísel, taková že

$\Large\frac pq=\sum_{n=1}^i\frac 1{a_n}\,.$

Pavel · 22. 01. 2011 22:24 — Editoval Pavel (22. 01. 2011 22:48)

Je zajímavé, že pomocí konečné sumy převrácených hodnot přirozených čísel $a_n$ lze kladná racionální čísla $\frac pq$
i za předpokladu, že 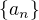$\{a_n\}$ je např. posloupnost kladných lichých čísel. Pak číslo 1 lze vyjádřit jako součet

$\Large 1=\frac 13+\frac 15+\frac 17+\frac 19+\frac 1{11}+\frac 1{13}+\frac 1{23}+\frac 1{721}+\frac 1{979007}+\frac 1{661211444787}+\frac 1{622321538786143185105739}+\nl +\frac 1{511768271877666618502328764212401495966764795565}+\nl +\frac 1{209525411280522638000804396401925664136495425904830384693383280180439963265695525939102230139815}$

OPRAVA: ne všechna racionální čísla lze takto vyjádřit.

petrkovar · 31. 01. 2011 14:36

Jeden pěkný induktivní důkaz je tady.

Matematické Fórum

#1 21. 01. 2011 14:53

matematická indukce

#2 21. 01. 2011 15:44

Re: matematická indukce

#3 21. 01. 2011 15:56

Re: matematická indukce

#4 21. 01. 2011 16:07

Re: matematická indukce

#5 21. 01. 2011 17:00

Re: matematická indukce

#6 21. 01. 2011 18:29

Re: matematická indukce

#7 21. 01. 2011 18:33

Re: matematická indukce

#8 22. 01. 2011 22:01

Re: matematická indukce

#9 22. 01. 2011 22:24 — Editoval Pavel (22. 01. 2011 22:48)

Re: matematická indukce

#10 31. 01. 2011 14:36

Re: matematická indukce

Zápatí