Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 02. 2011 15:49 — Editoval Maxim K (04. 02. 2011 15:50)
Derivace nespojitych funkci
Ahoj.
Par dni pred zkouskou jsem si (nejspise z duvodu pretlaku informaci na jednu neprospanou minutu) uvedomil, ze mam velice nezdravy zmatek v tematu derivaci nespojitych funkci. Obvykle jsem postupoval tak, ze jsem si nasel priklad a podle korektniho vysledku uvedeneho pod nim, jsem se snazil odvodit, jak se podobna vec ma resit. Bohuzel jsem postupem casu prisel na to, ze muj obecny postup nefunguje a proto se musim ptat. Vim, ze pravidla hovori o jedne otazce na tema, nicmene prislo by mi trochu matouci (zejmena pro me), kdybych sve otazky oddelil.
Jedna se mi zejmena o funkce, ktere jsou zadane v cele casti. Napriklad treti priklad zde:
http://www.karlin.mff.cuni.cz/~kalenda/ … 1/mi-c.pdf
Pokud je mi dobre znamo, cela cast je spojita zprava, nespojita zleva. Proto nerozumim zejmena tomu, proc je funkce nespojita v  zprava, jak je uvedeno dole ve vysledku.
zprava, jak je uvedeno dole ve vysledku.
Nyni k samotne derivaci - priznam se, nemam tuseni, proc je vysledek takovy, jaky je, zejmena v rozlozeni intervalu. Chapu, ze v 0 je derivace problemova, proto je potreba zde specialne provest kontrolu, ale konkretni hodnoty na ostatnich mistech obou intervalu - tomu nerozumim. Vychazim z predpokladu, ze cela cast nam hodnotu proste "zaokrouhli", tudiz se na oboru hodnot funkce arccos dostane na nejake prirozene cislo. Proc je ale takovy a takovy konkretni vysledek pro ony dva intervaly, na to jsem zatim neprisel. Zejmena pak ta 0 pro zaporny interval.
Velice podobne napriklad zde: opet treti priklad
http://www.karlin.mff.cuni.cz/~kalenda/ … 5/mi-c.pdf
Nerozumim, proc je pro hodnoty (2k + 1)pi predpis dervace 0, zatimco pro (2k-1)pi je 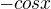 - oba vyrazy jsou prece liche nasobky pi.
- oba vyrazy jsou prece liche nasobky pi.
Tento pripad - opet treti priklad:
http://www.karlin.mff.cuni.cz/~kalenda/ … 1/mi-b.pdf
Proc se nespojitost funkce tyka pouze lichych cisel? Protoze pokud dosadime sude cislo, funkce sinus bude rovna hodnote 0, tudiz se cely vyraz "vynuluje"? Je to spravna myslenka?
A dalsi otazka k tomuto prikladu - proc derivace pro 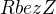 obsahuje samotne
obsahuje samotne 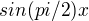 ? Z toho mi vyplyva, ze se z clenu, ktery by derivovan, stala jednicka - proc?
? Z toho mi vyplyva, ze se z clenu, ktery by derivovan, stala jednicka - proc?
Dekuji predem za jakoukoliv odpoved. Uvedl jsem zde tolik prikladu, abych dostatecne vysvetlil, cemu se snazim prijit na kloub. Verim, ze me kazda rada posune o neco blize pochopeni. Dekuji jeste jednou.
Offline
#2 04. 02. 2011 15:57
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Derivace nespojitych funkci
↑ Maxim K:
Alespoň na část odpovím:
f(x) = [x] je sice spojitá zprava, ale to protože f(x) = x je rostoucí funkce. Když se podíváte na ty hodnoty v odkazu, tak v -1 to je [2] arcsin(-1). Když ale x jakkoli málo zvětšíte od -1 směrem k nule, celá část ihned "skočí" na jedničku. Proto tam je nespojitá zprava.
Kdyžtak si ty jednotlivé úlohy hoďte do zvlášť témat, ať se to tu neplete v jednom. Nebo zde budem řešit jen to jedno a podle schopností můžete přidávat další (už ale do zvlášť témat).
Offline
#3 04. 02. 2011 16:26
Re: Derivace nespojitych funkci
↑ halogan:
Dekuji, rozumim. Jen hloupa otazka, proc po priblizeni se k nule skoci na jednicku? Proc ne na nulu? Myslim, ze cela cast ma obor hodnot v mnozine Z. Pokud by ma domnenka byla spravna, pak bych nejspis zacinal rozumet tem ruznym derivacim pro ruzne intervaly def. oboru. Pletu se?
A tykejte mi, prosim.
Offline
#5 05. 02. 2011 14:17
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Derivace nespojitych funkci
↑ Maxim K:
Pro (-1, 0) nám ta celá část dává jedničku, takže derivujeme jen ten arcsin, to je jasné?
Pro (0, 1) má arccos funkční hodnoty v intervalu (0, pi/2), takže když to pronásobíme s 2/pi), tak dostáváme hodnoty mezi 0 a 1, a jejich celá část je nula. Proto na (0, 1) bude ta funkce konstantní nulová, derivace tedy též nulová.
Offline
#7 07. 02. 2011 00:02
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Derivace nespojitych funkci
↑ Maxim K:
On tu hodnotu pí ale má jen a pouze v bodě -1, pro x větší než -1 už dostanete v celé části hodnotu ostře menší než 2. Proto tam není spojitá.
Offline