Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Anketa
Zdá se vám to těžké?
| ANO | 8% - 1 | |||||
| NE | 83% - 10 | |||||
| NEVIM | 0% - 0 | |||||
| NEROZUMIM ZADANI | 8% - 1 | |||||
| Počet hlasujících: 14 | ||||||
#3 05. 02. 2011 17:59 — Editoval claudia (05. 02. 2011 17:59)
Re: Lineární algebra
Ty komutující matice si představíme jako vektory a chceme dokázat, že i součet komutujících matic, popřípadně komutující matice vynásobená skalárem, též komutuje (to vyplývá z žádané definice podprostoru).
Mějme komutující matice X, Y. Pak  součet zjevně komutuje. Také po vynásobení skalárem matice komutují:
součet zjevně komutuje. Také po vynásobení skalárem matice komutují:  .
.
Víme, že inverzní matice s A jistě komutuje. Víme, že jedntková matice komutuje. Pokud by tedy dimenze byla 2, máme bázi. Mám i podezření, že by to tak mohlo být. Ale nejsem si ale jistá, jak tu dimenzi elegantně zjistit?
V nejhorším se dá prvky té matice označit jako a, b, c, d a řešit hrubou silou soustavu rovnic.
EDIT: Nebylo by možno změnit název tématu, třeba na podprostor komutujících matic? Lingebra je široké téma :-)
Offline
#4 06. 02. 2011 00:56
Re: Lineární algebra
↑ claudia:
Dokonce možná ještě jednodušším případem matice komutující s danou maticí je ona sama. Teď večer se mi ale po pár pokusech v Mathematice zdá, že by v maticích 2x2 mohlo platit něco takového jako že  jsou vždy lineárně závislé (a teď jsem už dokonce i přišel na to, proč - fakt to platí).
jsou vždy lineárně závislé (a teď jsem už dokonce i přišel na to, proč - fakt to platí).
Každopádně pokud se napíšou ty rovnice po otrockém vynásobení zleva a zprava a výsledky se porovnají, tak vyleze soustava 4 rovnic o 4 neznámých, po jejichž řešení zjistíme, že dimenze je opravdu jen 2.
Pěkný důvod, proč to nějak tak je, uvádí kolega BrozekP na konci tohoto tématu.
Offline
#5 06. 02. 2011 01:23
Re: Lineární algebra
↑ Olin:
Děkuji za odkaz :-) Ve skutečnosti jsem jej mezitím i sama našla, ale nevzdělaná v oblasti vlastních vektorů a vlastních čísel jsem to zdůvodnění zatím nepochopila :-) Ani z pohledu xxxxx by to tedy asi nebylo zjednodušení. Tedy pokud jej řešení ještě zajímá :-)
Postřeh, že matice je sama se sebou komutující, je výborný :-) Ta lineární závislost se dá ukázat nějak snadno? Na první pohled to nevidím (tedy bez použití dim=2 :-).
Offline
#6 06. 02. 2011 11:10 — Editoval Olin (06. 02. 2011 11:11)
Re: Lineární algebra
↑ claudia:
Bez použití dimenze 2 to asi nepůjde, protože ve vyšších to spíš neplatí. Ovšem pro bude ,
,
což se nahlédne rozepsáním do složek, je totiž dobré vědět, jak se u matic 2x2 rychle najde inverzní :-)
Offline
#7 06. 02. 2011 11:22
Re: Lineární algebra
↑ Olin:
Perfektní :-)
Já myslela bez banálního použití způsobem: máme prostor dimenze dvě -> žádné tři vektory nemohou být lineárně nezávislé -> E, A, A^-1 jsou lineárně závislé :-)
Offline
#8 06. 02. 2011 12:14
Re: Lineární algebra
Teď mě napadlo ještě lepší zdůvodnění (ovšem s využitím letní lingebry) - uvedená rovnost je ekvivalentní (po vynásobení M) s rovností ,
,
ovšem  je charakteristickým polynomem matice M, tedy podle Hamilton-Cayleyho věty dostaneme po dosazení
je charakteristickým polynomem matice M, tedy podle Hamilton-Cayleyho věty dostaneme po dosazení  nulovou matici.
nulovou matici.
Po troše zobecnění bychom dostali asi i to, že v maticích 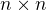 je
je  lineární kombinací
lineární kombinací  .
.
Offline

