Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz Vizingovy věty (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 02. 2011 18:46 — Editoval Olin (09. 02. 2011 18:46)
Důkaz Vizingovy věty
Zdravím kolegy. Pročítám si knížku Modern Graph Theory od B. Bollobáse a trochu jsem se zasekl u důkazu Vizingovy věty. Konkrétně jde o podtržené tvrzení. Jak může tvrdit, že se změna netýká hran s barvami  a
a 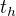 , když hrana
, když hrana 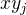 původně měla barvu
původně měla barvu 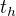 , ale byla přebarvena na
, ale byla přebarvena na 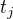 , naopak hrana
, naopak hrana 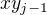 barvu
barvu 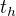 dostala?
dostala?
Možná jsem jen nepochopil, co přesně tím chce básník říct. Děkuji za jakoukoliv pomoc, vím, že je ten důkaz poměrně dlouhý.
Offline
- (téma jako vyřešené označil(a) Olin)
#3 09. 02. 2011 20:09
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Důkaz Vizingovy věty
Podle spojení "continue the recoloring" bych to chápal tak, že budu přebarvovat sice hrany i<h jak je psáno, ovšem už ne ty, které jsem předchozím kroku přebarvil (i<j). Rovněž si myslím, že graf H(s,th) je definován až na grafu, který vznikne po obarvení hran i<j.
"Máte úhel beta." "No to nemám."
Offline
#4 09. 02. 2011 20:23
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Důkaz Vizingovy věty
Když už jsem věnoval tolik času porozumění důkazu, tak alespoň potvrdím to, co píší kolegové. Podgraf H sestrojíme teprve po přebarvení hran 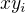 s
s 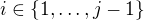 . Slova „This change“ se pak vztahují k obarvení hran
. Slova „This change“ se pak vztahují k obarvení hran 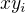 s
s 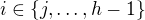
Offline
#5 09. 02. 2011 20:26 — Editoval Olin (09. 02. 2011 20:27)
Re: Důkaz Vizingovy věty
Hmm, už jsem asi přišel na to, v čem je ten vtip - 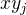 byl přebarven na "žádnou" barvu, teprv pak byl sestrojen
byl přebarven na "žádnou" barvu, teprv pak byl sestrojen 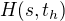 . Díky všem za podněty.
. Díky všem za podněty.
No není to zajímavá věta?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz Vizingovy věty (TOTO TÉMA JE VYŘEŠENÉ)
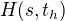 definoval až po přebarvení hran
definoval až po přebarvení hran 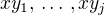 .)
.)