Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 19. 02. 2011 15:17 — Editoval VojtechSejkora (19. 02. 2011 15:18)
- VojtechSejkora
- Příspěvky: 176
- Reputace: 5
Re: exponencialní rovnice
↑ osamela:
nemžeš logaritmovat rovnici, pokud tam všude nemáš stejný základ....
takže já bych si to nejprve přepsal na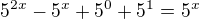 teď už můžeš logaritmovat
teď už můžeš logaritmovat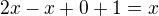 a odtud je viděť že to opravdu řešení nemá
a odtud je viděť že to opravdu řešení nemá
doufám že jsem to nějak nepopletl
Offline
#4 19. 02. 2011 15:22 — Editoval Pavel Brožek (19. 02. 2011 15:23)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: exponencialní rovnice
↑ VojtechSejkora:
Ne, takhle to opravdu nefunguje. Logaritmovat samozřejmě můžeš (za předpokladu, že obě strany jsou kladné), ale nevznikne z toho to, co píšeš, ale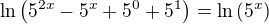
což je nám k ničemu.
Offline
#5 19. 02. 2011 15:22 — Editoval Hudler (19. 02. 2011 15:25)
Re: exponencialní rovnice
Ta jednička patří do exponentu předpokládám.
Převeď na stejný základ (5) a zaveď substituci (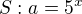 ). Dostaneš kvadratickou rovnici o neznámé a. Dojdeš k řešení a = ... a vrátíš substituci.
). Dostaneš kvadratickou rovnici o neznámé a. Dojdeš k řešení a = ... a vrátíš substituci.
//VojtechSejkora: Nejsou tam součiny...
Offline
#7 19. 02. 2011 15:26 — Editoval VojtechSejkora (19. 02. 2011 15:26)
- VojtechSejkora
- Příspěvky: 176
- Reputace: 5
Re: exponencialní rovnice
↑ Hudler:
ou kde jsi sebral že ji tam někde vychází  ?
?
kyby jsi napsal 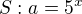 tak to už chápu
tak to už chápu
↑ Pavel Brožek:
aha díky
Offline
#8 19. 02. 2011 15:36 — Editoval VojtechSejkora (19. 02. 2011 15:37)
- VojtechSejkora
- Příspěvky: 176
- Reputace: 5
Re: exponencialní rovnice
↑ osamela:
takže ta rovnice vypadá takto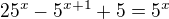
jednoduše upravíme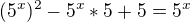
zavedeme supstituci 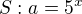
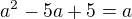
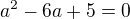
teď spočteš z kvadratické rovnice  a
a 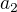
diskriminant je 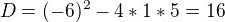
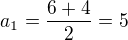
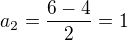
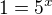 a
a 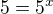
z toho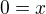 a
a 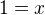
prosím Pavel Brožek o zkontrolování, ale myslím že už to mám správně:)
Offline
#9 19. 02. 2011 15:39 — Editoval Pavel Brožek (19. 02. 2011 15:41)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: exponencialní rovnice
↑ VojtechSejkora:
Souhlasím.
(Jinak, mé jméno se skloňuje běžně podle pravidel českého pravopisu :-) )
(A ještě jedna poznámka – je lepší psát \cdot místo * pro násobení. vypadá to mnohem lépe :-) )
Offline
#10 19. 02. 2011 15:52
- VojtechSejkora
- Příspěvky: 176
- Reputace: 5
Re: exponencialní rovnice
↑ Pavel Brožek:
s tím nesouhlasím:D třeba mě se lépe čte ta * jak tečka:D
Offline
#11 19. 02. 2011 15:57
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: exponencialní rovnice
↑ VojtechSejkora:
Dobře, tak jiný, lepší argument: Znak hvězdičky  se pro násobení v matematice standardně nepoužívá.
se pro násobení v matematice standardně nepoužívá.
Offline
#12 19. 02. 2011 16:03
- VojtechSejkora
- Příspěvky: 176
- Reputace: 5
Re: exponencialní rovnice
↑ Pavel Brožek:
njn ale zas u programování je běžně používá  (hvězdička) :p takže to není mco dobrý argument:)
(hvězdička) :p takže to není mco dobrý argument:)
Offline
#13 19. 02. 2011 16:07
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: exponencialní rovnice
↑ VojtechSejkora:
A my tady programujeme? Když budeš psát matiku v textu, jako třeba 5*7=35, nebo v kódu [ code]a:=7*b;[ /code], tak nic neřeknu. Ale pokud sázíme matematiku…
Ale nechme toho, piš si to jak chceš, dál už tě s tím otravovat nebudu :-).
Offline