Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 02. 2011 19:29
Analytické geometrie - shodnost z v E^2
Dobrý večer, mohla bych vás moc laskavě poprosit, jestli by jste mi to ochotně řekl, jak to počítá...dlouho jsem si přemýšlela už půl dne a hledala jsem přes internetu ani ve skriptě...nic jsem nenašla. Prosím, poraďte mi.
z = z_2 o z_1
z_1(x,y) = (-y+6 , x) a z_2(x,y) = (y , -x)
z = z_2 * (-y+6 , x) = (y , -x)*(-y+6 , x) = (-2y+6, -2x)
Promiň, já tomu nerozumím. Děkuji za pomoc.
Offline
#4 21. 02. 2011 09:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analytické geometrie - shodnost z v E^2
↑ zdenek1: děkuji velmi.
↑ Verena:
Tento obor matematiky jsem nikdy nestudovala, přímo k úloze asi pořádný výklad neposkytnu (musela bych si to nastudovat a asi by mi to nešlo). Snad něco najdeš v této sbírce odkazů nebo kolegové doplní (kolegům děkuji).
Ať se vede.
Offline
#5 21. 02. 2011 12:28 — Editoval Cynyc (21. 02. 2011 12:29)
Re: Analytické geometrie - shodnost z v E^2
Takže úplně polopatě: skládání zobrazení je dosazení jednoho do druhého, přesněji pravého do levého. Takže když si rozepíšu po složkách 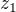
a 
a dosadím za x,y do druhého zobrazení x',y' z prvního zobrazení (to je to složení), dostanu
,
což je předpis složeného zobrazení  (a jestli to dobře chápu, to, co nazýváte transformačními rovnicemi), které můžu zpátky vyjádřit ve vektorové formě jako
(a jestli to dobře chápu, to, co nazýváte transformačními rovnicemi), které můžu zpátky vyjádřit ve vektorové formě jako  . Typ zobrazení tu lze určit jednoduchou úvahou: zobrazím-li bod [x,y], pak se x-ová souřadnice nezmění, ale y-ová se zmenší o 6. Dojde tedy k posunutí (což je typ zobrazení) o vektor (0,6) (určující prvek). Takhle jednoduché je to ale jen u posunutí, u ostatních shodností je třeba znát obecný tvar jejich předpisu, nejčastěji ve formě matice.
. Typ zobrazení tu lze určit jednoduchou úvahou: zobrazím-li bod [x,y], pak se x-ová souřadnice nezmění, ale y-ová se zmenší o 6. Dojde tedy k posunutí (což je typ zobrazení) o vektor (0,6) (určující prvek). Takhle jednoduché je to ale jen u posunutí, u ostatních shodností je třeba znát obecný tvar jejich předpisu, nejčastěji ve formě matice.
Offline
#9 21. 02. 2011 20:24 — Editoval Dana1 (21. 02. 2011 22:03)
- Dana1
- Host
Re: Analytické geometrie - shodnost z v E^2
↑ Verena:
Študovala som Matfyz, ale dávno a toto sme nebrali.
Len som si naštudovala, čo Ti radil Cynyc a zdá sa mi, že to zloženie v 2. príklade na veľkom bielom papieri, čo si dala na kontrolu máš dobre.
To pokračovanie už neviem, čo je ...
Nechcem Ťa mýliť, ale našla som o stredovej súmernosti pod číslom 3.1.4 takéto niečo. Netuším, čo to je, ale netýka sa to toho Tvojho 1. príkladu na veľkom bielom papieri, čo si dala na kontrolu? Mal by to byť predpis, ako sa zobrazuje bod v stredovej súmernosti, alebo nie?
Mne to priradenie tak vychádza, keď si to skúšam. ( x0, y0 sú súradnice stredu S )
Ak by to bolo dobre, predpis pre z1 by bol (-x + 4; -y + 2) predpis pre z2 by bol (-x + 2, -y -6), skladanie sa robí rovnako ako v predchádzajúcom príklade.
Ak Ťa mýlim, prepáč...
#10 10. 03. 2011 15:05 — Editoval Kondr (10. 03. 2011 15:09)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Analytické geometrie - shodnost z v E^2
↑ Verena: K prvnímu viz ↑ Dana1: (rada je dobře), ke druhému: rovnice vyšly stejně. Jde o otočení, střed máš nalezený dobře, úhel by se dopočítal pomocí matice rotace 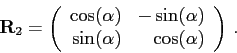 -- známe prvky matice, dopočíst alfu je snadné. Pokud jsem ale pochopil zadání, alfu ani S jsme hledat nemuseli.
-- známe prvky matice, dopočíst alfu je snadné. Pokud jsem ale pochopil zadání, alfu ani S jsme hledat nemuseli.
Ať se daří.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
![kopírovat do textarea $A[x_0;y_0]$](/mathtex/63/63fb6ceb15daa6f8b7bd2710db5fe273.gif) se v
se v ![kopírovat do textarea $A^\prime[6-y_0;x_0]$](/mathtex/be/be4f3a2251d33e8dcfca018784110840.gif) a ten se v
a ten se v ![kopírovat do textarea $A^{\prime\prime}[x_0;y_0-6]$](/mathtex/37/378421c3bec3f247fe8b455f59ad27ff.gif)
