Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 05. 2008 16:26 — Editoval atn.hvc (22. 05. 2008 16:27)
Vyšetření funkce
ahoj, pokusil jsem se vysetrit funkci, ale vubec netusim, jestli to mam spravne, tak bych vas chtel pozadat o kontrolu.
diky
zadana funkce:![kopírovat do textarea $f(x) = \sqrt[3]{(x+1)^2}-\sqrt[3]{(x-1)^2}$](/mathtex/4d/4d4eebe93c8cf88f5ba0547e7a9a7b21.gif)
1) D(f)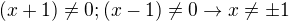
D(f)=R \ {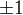 }
}
2) kde je f spojita:
fce je spojita na D(f)
3) zda je f suda, licha, zda je f periodicka 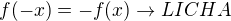
![kopírovat do textarea $\sqrt[3]{(-x+1)^2}-\sqrt[3]{(-x-1)^2}$](/mathtex/9e/9e6e51e0b758de4bfba00ae263d32288.gif)
4) f' a body podezrele z extremu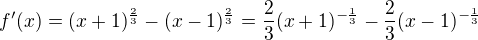
![kopírovat do textarea $0={\frac{2}{3}}({\frac{1}{\sqrt[3]{x+1}}}-{\frac{1}{\sqrt[3]{x-1}})} \rightarrow x+1=x-1\rightarrow+1=-1$](/mathtex/37/376b6cdecdaf5cd789ce85d715c43b82.gif) ...stale roustouci, extremy nejsou
...stale roustouci, extremy nejsou
5) intervaly ryzi monotonie a lokalni extremy f
NEJSOU (tady si nejsem jist, jestli je to spravne)
6) f'' a body podezrele z inflexe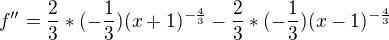

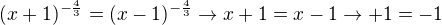 ...STALE KONVEXNI, NEMA INFLEXNI BODY
...STALE KONVEXNI, NEMA INFLEXNI BODY
7) intervaly ryzi konvexnosti a ryzi konkavnosti a inflexni body![kopírovat do textarea ${\lim}\limits_{x \to 1}(\sqrt[3]{(x+1)^2}-\sqrt[3]{(x-1)^2})={\lim}\limits_{x \to 1}(0-\sqrt[3]{4)}=-\sqrt[3]{4}$](/mathtex/1b/1bb98a73d672de8d7b6337958d13aa0d.gif)
![kopírovat do textarea ${\lim}\limits_{x \to 1}(\sqrt[3]{(x+1)^2}-\sqrt[3]{(x-1)^2})=-\sqrt[3]{4}$](/mathtex/96/9663f5b87baa76ef6aa94423a87fbb34.gif)
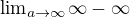 ...NENI DEFINOVANO
...NENI DEFINOVANO
8) svisle asymptoty a asymtoty v +- nekonecnu, neexistuji-li asymptoty, urcime jednostranne limity v krajnich bodech D(f) a v bodech nespojitosti f...
sikma: y=ax+b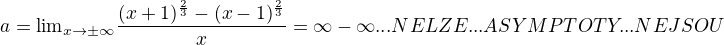
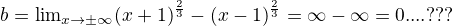
9)...pripadne pruseciky s osami, funkcni hodnoty ve vyznamnych bodech,...nacrtneme graf
x=0
pocatek soustavy souradnic [0,0]
FUNKCE RENDEROVANA POCITACEM
nevim jestli souhlasi
Offline
#2 22. 05. 2008 17:30
Re: Vyšetření funkce
je v tom dost hokej. v prvnim bodu: proc jsi vyloucil z definicniho oboru x = -1, x = 1? pak ve 4. bodu: jak z vysledku 1 = -1 plyne, ze funkce je na celem definicnim oboru rostouci? navic, co to znamena, ze 1 = -1? dal uz jsem to moc nezkoumal, ale u tech limit: kdyz je limita typu  , tak jsi napsal "nelze". co to znamena, ze nejde dopocitat?
, tak jsi napsal "nelze". co to znamena, ze nejde dopocitat?
Offline
 proste neni definovano, tak nevim no
proste neni definovano, tak nevim no