Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 05. 2008 11:18
Rovnice s kombinačními čísly
ahoj... mám problém. Nemůžu nikde vyčíst jak se dělají rovnice s kombinačními čísly... Neumíte to někdo vysvětlit pro hlupce jako jsem já? Dík...
Mám tady třeba x nad (x-2) = 6 ... pořád na to nemůžu přijít, i když je to primitivní. Dík
Offline
#5 22. 05. 2008 18:27
#6 23. 05. 2008 00:18
Re: Rovnice s kombinačními čísly
Nechci aby to tu za mě někdo řešil... jde jen o ukázkovej příklad, no... nechci aby to za mě někdo vyřešil... jen potřebuju nakopnout a ostatní mi už snad půjdou.... ostatně jsem si myslela, že tyhle stránky jsou na pomoc lidem, kteří zrovna matematiční talenti nejsou.... ale omlouvám se, jestli to tu nějak narušuju.... :(
Offline
#7 23. 05. 2008 06:43
Re: Rovnice s kombinačními čísly
↑ Janča09:Zdravím , posílám jen pár typů . Jsou to jen příklady . Ostatní se pak řeší analogicky . Pomůže ti to ?

Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#9 23. 05. 2008 10:00
Re: Rovnice s kombinačními čísly
↑ Janča09:
tak sem nejakej ten priklad napis, marne premejslim jak to vysvetlit obecne. na prikladu ti to snad vysvetlim.
Offline
#10 23. 05. 2008 10:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice s kombinačními čísly
Zdravim :-) ocisluji jednotlive kroky a ty napises, ktery neni jasny, OK? - to je tvoje rovnice
- to je tvoje rovnice
1. budu rozepisovat pouze 1. zavorku - vsechno delam jako kombinacni cislo, n=x-1, k=x-2 - kopirovano z wikipedie
- kopirovano z wikipedie upravuji pouze dolni pravou zavorku
upravuji pouze dolni pravou zavorku
2. 
3.  rozepisi "vetsi faktorial" do nasobku tak dlozho, az mam mensi faktorial, abych mogla kratit
rozepisi "vetsi faktorial" do nasobku tak dlozho, az mam mensi faktorial, abych mogla kratit
4. 
5. 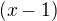 - toto je prvni zavorka po uprave. stejne upravim druhou zavorku, davam velky pozor na znamenka, musim brat v uvahu definicni obor pro x. OK?
- toto je prvni zavorka po uprave. stejne upravim druhou zavorku, davam velky pozor na znamenka, musim brat v uvahu definicni obor pro x. OK?
Offline
#11 23. 05. 2008 10:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice s kombinačními čísly
↑ Alesak:
Zdravim :-) sice, mela bych rici - "chod studovat literaturu", ale budu rada, kdyz kolegyni pohlidas - at se na nas nezlobi :-) . Mam to vsechno spravne?
Offline
#12 23. 05. 2008 10:39
Re: Rovnice s kombinačními čísly
↑ jelena:
taky zdravim :) mas to cely dobre.
jeste doplnim ze tady je dobry pouzit pravidlo  , takze
, takze  , kde n = x - 1, a k = x - 2. to pravidlo(stejne jako spousta ostanich) se da vycist z pascalova trojuhelnika.
, kde n = x - 1, a k = x - 2. to pravidlo(stejne jako spousta ostanich) se da vycist z pascalova trojuhelnika.
a tu literaturu bych se mel vazne jit ucit, ze slohovy casti se mi poved plnej pocet:(
Offline




