Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 03. 2011 12:03
Termika, šíření tepla
Najděte rozložení teploty T v závislosti na R v prostoru mezi dvěma soustřednými koulemi o poloměru R_1 a R_2, který je homogenně vyplněn látkou schopnou vést teplo, za podmínky, že teplota je stálá a rovna T_1 respektive T_2.
Děkuju za pomoc, jako jediný mi z kapitoly tento příklad stále odolává:-)
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
- (téma jako vyřešené označil(a) Esperance)
#2 06. 03. 2011 07:41
Re: Termika, šíření tepla
↑ Esperance:
Myslím, že by mělo stačit vyřešit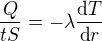 , když
, když 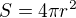
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 06. 03. 2011 14:25
Re: Termika, šíření tepla
↑ Esperance: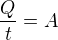 (abych se stím pořád nepsal)
(abych se stím pořád nepsal)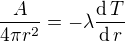
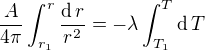
![kopírovat do textarea $\frac{A}{4\pi}\left[\frac1{r_1}-\frac1r\right]=\lambda(T_1-T)$](/mathtex/24/241278d14b478e8c45ae040a1da3182a.gif) (1)
(1)
Nyní speciálně pro 
![kopírovat do textarea $\frac{A}{4\pi}\left[\frac1{r_1}-\frac1{r_2}\right]=\lambda(T_1-T_2)$](/mathtex/a0/a0f6657780a35a6c9087f52e34aeaf34.gif) (2)
(2)
Řekl bych, že dělením  a trochou úprav dostaneš požadovaný výsledek (ale to už jsem nepočítal)
a trochou úprav dostaneš požadovaný výsledek (ale to už jsem nepočítal)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline

