Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 03. 2011 14:27 — Editoval Alivendes (21. 03. 2011 14:28)
Tayloří Polynom
Zdravím, zabýval jsem teď rozvojem funkcí v nekonečné řady a chtěl bych se zeptat jak se myslí to, že funci lze rozvninout v taylorovu řadu pouze v případě všech derivací.
Mě se zajímá když je třeba třetí derivace nule a tak čtvrtá je taky nula nebo neexistuje. Děkuji ...
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#2 21. 03. 2011 14:40 — Editoval musixx (21. 03. 2011 14:42)
Re: Tayloří Polynom
Taylorův polynom je aproximace funkce v bodě (a jeho okolí). A derivace jsou potřeba jen v tom jednom bodě a jen jejich hodnoty (při typickém značení se tam vyskytují členy 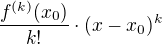 . Z toho, že třeba
. Z toho, že třeba 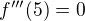 neplyne nic o tom, kolik je
neplyne nic o tom, kolik je 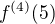 , může to být klidně 28, není pravda, že by to muselo být zase nula nebo že by tam čtvrtá derivace vůbec nemohla existovat.
, může to být klidně 28, není pravda, že by to muselo být zase nula nebo že by tam čtvrtá derivace vůbec nemohla existovat.
EDIT: Jo kdyby na nějakém okolí byla třeba třetí derivace jako funkce stále rovna nule, pak by i všechny ostatní derivace tam nulové byly. To se ti asi trochu smíchalo.
Offline
#3 21. 03. 2011 15:03 — Editoval Rumburak (21. 03. 2011 15:21)
Re: Tayloří Polynom
Pokud jde o (nekonečnou) T. řadu:
Konečné derivace všech řádů v bodě x = a, který je tzv. středem rozvoje, požaduje definice T. řady .
Tato řada může na nějakém okolí středu konvergovat k původní funkci nebo také nemusí.
K tomu, abychom mohli pozitivně vyřešit otázku, zda skutečně
(1) na určitém okolí středu je součet nekonečné T. řady roven dané funkci,
nám výrazným způsobem pomůže, když daná funkce má konečné derivace všech řádů na celém tomto okolí.
Je to dokonce nutná podmínka (ne však postačující) pro to, aby výrok (1) platil.
Viz Odkaz .
Offline
#5 21. 03. 2011 15:47
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Tayloří Polynom
↑ Alivendes:
Ty derivace existují, jen jsou nulové. A ono je celkem zbytečné aproximovat polynom (prvního stupně) Taylorovým polynomem... protože dostaneš v tomhle případě to samé.
Offline
#6 21. 03. 2011 15:52
Re: Tayloří Polynom
↑ halogan:
Děkuji, teď je mi to jasné.
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#7 21. 03. 2011 16:07
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Tayloří Polynom
↑ Alivendes:
Jak se to postupně přibližuje je vidět na ukázkách od Wolfram Inst., kde si můžeš stáhnout jejich Mathematica Player a pak si stahovat různé ukázky. Tady je video s Taylorovým polynomem. V tom Playeru máš šoupátka, kde měníš stupeň rozvoje. Je to taková zábavná výuka, člověk u toho může svačit a s blaženým úsměvem oslavovat vítězství nad matematickou látkou.
A taky nezapomeň rozlišovat Taylorův polynom a Taylorův rozvoj. To první je jen polynom s těmi spočtenými koeficienty, to druhé je polynom + funkce chyby. Funkční hodnota toho prvního se nemusí rovnat v každém bodě, zatímco to druhé se rovná (díky té funkci chyby).
Já třeba tyto dva pojmy často nerozlišuju, a vytvářím tak zbytečný bordel.
Offline