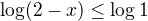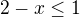Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 22. 03. 2011 07:41 Příspěvek uživatele Cast byl skryt uživatelem Cast. Důvod: chybí návaznost
#3 22. 03. 2011 07:44
Re: Definiční obor funkce
↑ Cast:
Máš tam zlomek, tedy jmenovatel nemůže být roven 0, to je další podmínka kterou se musíš zabývat
A další podmínka bude celá odmocnina, protože je to druhá odmocnina nemůže pod ní být záporné číslo
Offline

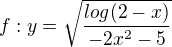
 to je jasné, ale co dál?
to je jasné, ale co dál?
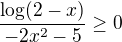
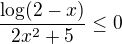
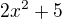 je vždy kladné, musí být
je vždy kladné, musí být