Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 03. 2011 19:45 — Editoval Pavel Brožek (22. 03. 2011 20:38)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Najděte funkční závislost
Mějme diferenciální rovnici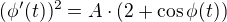 ,
,
kde  je konstanta, s počáteční podmínkou
je konstanta, s počáteční podmínkou 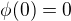 a
a  . Předpokládejme, že
. Předpokládejme, že 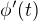 je spojitá funkce.
je spojitá funkce.
Funkce 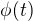 je zřejmě rostoucí. Číslo t, ve kterém funkce
je zřejmě rostoucí. Číslo t, ve kterém funkce 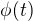 nabývá hodnoty
nabývá hodnoty  zřejmě závisí na konstantě A, značme ho
zřejmě závisí na konstantě A, značme ho 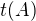 . Pokuste se co nejlépe popsat chování funkce
. Pokuste se co nejlépe popsat chování funkce 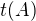 . (Tím myslím, abyste zapsali funkci
. (Tím myslím, abyste zapsali funkci 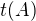 pomocí elementárních funkcí.)
pomocí elementárních funkcí.)
(Tuším, jaké je řešení, ale zatím to nedokážu dokázat. [Edit: teď už to umím dokázat.] Úloha pochází z řešení fyzikálního modelu, z toho se dá závislost uhádnout.)
Offline
#2 21. 03. 2011 20:30
- check_drummer

- Příspěvky: 5168
- Reputace: 106
Re: Najděte funkční závislost
↑ Pavel Brožek:
Je ona diferenciální rovnice řešitelná v uzavřeném tvaru? Pokud ano, má být nalezení jejího řešení součástí řešení celé úlohy nebo je možno ho uvést (jako hint)?
"Máte úhel beta." "No to nemám."
Offline
#3 21. 03. 2011 20:41
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Najděte funkční závislost
↑ check_drummer:
Mathematica mi dává řešení pomocí funkce JacobiAmplitude. Spíš by mě zajímalo, jestli jde závislost nějak elegantně určit bez vyřešení rovnice.
Offline
#4 22. 03. 2011 16:00
- check_drummer

- Příspěvky: 5168
- Reputace: 106
Re: Najděte funkční závislost
↑ Pavel Brožek:
Z čeho prosím plyne, že je funkce rostoucí? Díky.
"Máte úhel beta." "No to nemám."
Offline
#5 22. 03. 2011 20:35
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Najděte funkční závislost
↑ check_drummer:
Omlouvám se za nepřesnost. Že je funkce 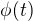 rostoucí není vůbec zřejmé, pokud vůbec je nutně rostoucí, nenašel jsem způsob, jak to ukázat.
rostoucí není vůbec zřejmé, pokud vůbec je nutně rostoucí, nenašel jsem způsob, jak to ukázat.
Předpokládejme tedy, že 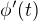 je spojitá funkce. Pak už to snad zřejmé opravdu je. (Opravil jsem zadání.)
je spojitá funkce. Pak už to snad zřejmé opravdu je. (Opravil jsem zadání.)
Offline