Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 03. 2011 14:57 — Editoval claudia (27. 03. 2011 15:01)
Re: Limita
Buď použitím vzorce 
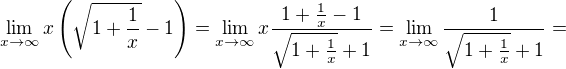
Nebo za aplikací l'Hospitalova pravidla
Offline
#3 27. 03. 2011 15:53
Re: Limita
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline



![kopírovat do textarea $
\lim_{x\to\infty} x \(\sqrt{1+\frac{1}{x}} - 1\)=\[\text{subst. }x=1/y\]\lim_{y\to 0^+} \frac{\sqrt{1+y} - 1}y
$](/mathtex/97/97bc68b0d28e572f845d75e1af7706d7.gif)