Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrace: Najdete a, tak aby platilo (TOTO TÉMA JE VYŘEŠENÉ)
#4 03. 04. 2011 16:34
- Dana1
- Host
Re: Integrace: Najdete a, tak aby platilo
↑ Majkl9102:
To je tuším rozklad na parciálne zlomky...
#5 03. 04. 2011 18:49 — Editoval jarrro (03. 04. 2011 18:50)
Re: Integrace: Najdete a, tak aby platilo
↑ Majkl9102:↑ Dana1:áno je to rozklad na parciálne zlomky
MATH IS THE BEST!!!
Offline
#6 04. 04. 2011 16:08
Re: Integrace: Najdete a, tak aby platilo
↑ jarrro: mohl by jsi to tady vypočítat celý tu integraci, parcialní zlomky jsem ještě nepoužíval, nebo aspoň nevím že bych je někdy použil. Ikdyž jsem se teď na ně díval ke správnemu výsledku jsem se nedostal. předem děkuju
Offline
#7 04. 04. 2011 18:42 — Editoval claudia (04. 04. 2011 18:46)
Re: Integrace: Najdete a, tak aby platilo
Existují na to formální postupy, ale v takto jednoduchém případě to jde i uhodnout:
(http://www.mojeskola.cz/Vyuka/Php/Learn … rokem9.php)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrace: Najdete a, tak aby platilo (TOTO TÉMA JE VYŘEŠENÉ)


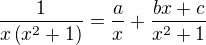 nájdi a,b,c a len potom integruj
nájdi a,b,c a len potom integruj