Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 05. 04. 2011 21:47
Re: Vrchol paraboly
↑ joinusman:
Tohle je trochu přehlednější
http://maths.cz/clanky/analyticka-geome … abola.html


![kopírovat do textarea $V[-2, -4+c]$](/mathtex/13/1300af38c2242dac0ec97427929107f5.gif)
![kopírovat do textarea $F[-2,0]$](/mathtex/fa/fa880a80ae8d21a4000a2a13c67c84c0.gif)
 podle vzorcu z odkazu je
podle vzorcu z odkazu je 



snad jsem to přepsala bez chyb
...a zkusil si použít trojčlenku? :)
Offline
#5 05. 04. 2011 21:49
Re: Vrchol paraboly
↑ joinusman:
Parabola má obecně tvar  , kde
, kde ![kopírovat do textarea $V[m,n]$](/mathtex/4a/4a80ec0b861d2d60bf256f847689d5e5.gif) je vrchol.
je vrchol.  ová souřadnice ohniska a vrcholu je stejná, tj.
ová souřadnice ohniska a vrcholu je stejná, tj. 
Bude tedy 
Když to porovnám se zadanou rovnicí  , tak vidím, že
, tak vidím, že

Je tedy 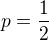
Protože vzdálenost  , bude
, bude 
![kopírovat do textarea $V[-2;-\frac14]$](/mathtex/82/82d63bf4660e68a45135a1a77e5299fc.gif)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
 , c je reálný parametr.
, c je reálný parametr.
