Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Extenze teorie následníka s nulou o konstantní symbol (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 04. 2011 22:14
Extenze teorie následníka s nulou o konstantní symbol
Zdravím, potřeboval bych poradit.
Máme danou teorii následníka s nulou  :
:
Jazyk: <S,0>, S je unární funkční symbol, 0 je konstantní symbol.
Axiomy: (Q1) 
(Q2) 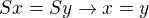
(Q7) 
SC-schema: 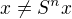 ; n > 0 je přirozené.
; n > 0 je přirozené.
Pro n přirozené je n-tý numerál  konstantní term S...S0, S aplikováno n-krát;
konstantní term S...S0, S aplikováno n-krát; 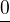 je 0.
je 0.
A s následujícím si nějak vůbec nevím rady:
1. Nechť T je extenze teorie následníka s nulou  o nový konstantní symbol c.
o nový konstantní symbol c.
a) Dokažte či vyvraťte, že T je kompletní.
b) Nalezněte všechny jednoduché kompletní extenze T.
c) Určete izomorfní spektrum T.
d) Zjistěte, zda T je ekvivalentní otevřené teorii.
e) Zjistěte, zda T je ekvivalentní konečně axiomatizovatelné teorii.
2. Zvolte si jednu jednoduchou kompletní extenzi T' teorie T z předchozího příkladu.
a) Nalezněte algebraický prvomodel teorie T'; případně dokažte, že neexistuje.
b) Zjistěte, zda T' je modelově kompletní.
Offline
- (téma jako vyřešené označil(a) nordec)
#5 01. 05. 2011 18:49
Re: Extenze teorie následníka s nulou o konstantní symbol
Tak konečně se na to vrhnu:-) Většina věcí je podobná jako na tom odkazu co jsem posílal v předchozím příspěvku...
1.
a) teorie T není kompletní. Není dokazatelná ani vyvratitelná například formule 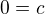 (protože
(protože  může být zvoleno libovolně)
může být zvoleno libovolně)
b) zkompletnit tuto teorii jde nejednodušeji tak že se přidá jeden axiom 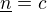 pro některé n. Tím jsem vytvořil spočetně mnoho různých zůplnění.
pro některé n. Tím jsem vytvořil spočetně mnoho různých zůplnění.
Dále se dá zůplnit přidáním schématu  pro n přirozené.
pro n přirozené.
Poslední jednoduché zůplnění (ale takové, které ti asi nebude uznáno) je přidáním  . Takto rozšířená teorie je sporná, takže úplná:-)
. Takto rozšířená teorie je sporná, takže úplná:-)
c) izomorfní spektrum je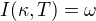 pro kapa nekonečné a
pro kapa nekonečné a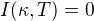 pro kapa konečné.
pro kapa konečné.
Zdůvodní se to takto: pro kapa konečné, modely neexistujou.
Pro kapa spočetné jsou modely následující:
jedna možina N (přirozená čísla) a nejvýše spočetně mnoho množin Z (celá čísla). Zatím nebudu uvažovat konstantu c. Takových modelů je  . Nyní budu uvažovat konstantu c. Ta může být buď v množině N a nebo v některé množině Z. V množině N může nabývat jedné z
. Nyní budu uvažovat konstantu c. Ta může být buď v množině N a nebo v některé množině Z. V množině N může nabývat jedné z  hodnot. Pokud je v některé množině Z, tak nejde nijak rozlišit jaké hodnoty nabývá (nemáme uspořádání), takže je jen jedna možnost. Tudíž všech modelů je
hodnot. Pokud je v některé množině Z, tak nejde nijak rozlišit jaké hodnoty nabývá (nemáme uspořádání), takže je jen jedna možnost. Tudíž všech modelů je 
Pro kapa nespočetné je bez uvažování konstanty c jen jedna možnost. Jedna množina N a kapa množin Z. No a podobně jako v předchozím případě lze uvažovat jakou hodnotu může nabývat konstanta c. Stejnou úvahou zjistíme, že modelů je  .
.
d) to je stejný problém jako u kolegyně. Pořád se mi nepovedlo najít co znamená otevřená teorie, pokus se zapátrat v poznámkách, případně doplním
e) T není konečně axiomatizovatelná.
Důkaz: Uvažujme konečně axiomatizovanou teorii TFin (ekvivalentní). Přidáním axiomu 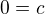 získáme opět konečně axiomatizovanou teorii TFin0. Pokud této teorii nyní ochudíme jazyk o konstantu c, a ve všech axiomech ji nahradíme konstatnou 0 získali jsme opět konečně axiomatizovanou teorii TFin0-. Tato teorie je ale ekvivalentní teorii
získáme opět konečně axiomatizovanou teorii TFin0. Pokud této teorii nyní ochudíme jazyk o konstantu c, a ve všech axiomech ji nahradíme konstatnou 0 získali jsme opět konečně axiomatizovanou teorii TFin0-. Tato teorie je ale ekvivalentní teorii  která není konečně axiomatizovatelná. Což je spor.
která není konečně axiomatizovatelná. Což je spor.
2. zvolím si rozšíření o axiom 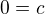
takto rozšířená teorie je (v podstatě) ekvivalentí teorii  . A stejně jako ona má algebraický prvomodel a je modelově kompletní
. A stejně jako ona má algebraický prvomodel a je modelově kompletní
a) algebraickým prvomodelem je model <N,S,0,c>
b) mně nenapadá jako to ještě zdůvodnit
Dva jsou tisíckrát jeden.
Offline
#6 02. 05. 2011 14:33
Re: Extenze teorie následníka s nulou o konstantní symbol
↑ Wotton:
Moc děkuji. Teď, když vidím, jak se řeší konkrétní příklad i s mně srozumitelnými vysvětleními, je i ta teorie okolo zase o trochu jasnější.
K 1d) jsem našel toto: otevřená teorie je taková teorie, jejíž všechny axiomy jsou otevřené formule.
Offline
#7 07. 05. 2011 15:28
Re: Extenze teorie následníka s nulou o konstantní symbol
Tak k 1d)
konečně jsem si našel čas a vlez do literatury (bohužel jsem musel, sice po tom co píšeš jsem si už vzpomněl, že jsem to někdy viděl, ale už si to pořádně nepamatuju).
Mělo by to být takhle.
Teorie  je ekvivalentní otevřené teorii. To znamená, že všechny její axiomy jsou ekvivalentní nějaké otevřené formuli (dokonce otevřené sentenci). V teorii rozšířené o konstantní symbol c jsme však nepřidali žádný axiom (pouze rozšířili jazyk), tudíž i nově vzniklá teorie je ekvivalentní otevřené teorii.
je ekvivalentní otevřené teorii. To znamená, že všechny její axiomy jsou ekvivalentní nějaké otevřené formuli (dokonce otevřené sentenci). V teorii rozšířené o konstantní symbol c jsme však nepřidali žádný axiom (pouze rozšířili jazyk), tudíž i nově vzniklá teorie je ekvivalentní otevřené teorii.
Aspoň už budu vědět co to znamená až se to tu objeví příště:-)
Dva jsou tisíckrát jeden.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Extenze teorie následníka s nulou o konstantní symbol (TOTO TÉMA JE VYŘEŠENÉ)
