Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Slovni uloha - rotacni kuzel, rotacni valec (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 05. 2008 16:08
- Slabsí matematik
- Příspěvky: 29
- Reputace: 0
Slovni uloha - rotacni kuzel, rotacni valec
Do rotacniho kuzele o polomeru podstavy R a výsce h vepiste rotacní válec, který má
nejvetsi obsah pláste (bez podstav).
Vim ze objem rotacniho kuzele je V= 1/3*pi*r^2*h
a obsah plaste rotacniho valce bez podstav , myslim: S=2*pi*r*h
ale jak ted na to kdyz nemam zadan ani obsah plaste ani objem, alespon jedno cislo. Mozna bych mohla vyjadrit h z jedne rovnice a dosadit do druhe, ale nevim...
dekuji za radu
Offline
#2 18. 05. 2008 19:10
Re: Slovni uloha - rotacni kuzel, rotacni valec
Ta úloha je analogická k vepisování obdélníku do rovnoramenného trojúhelníka. Náčrt:
Obsah pláště je 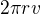 , ovšem díky vepsání do kužele je dán pevný vztah mezi r a v, a to
, ovšem díky vepsání do kužele je dán pevný vztah mezi r a v, a to 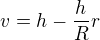 . Toto dosadíme do předchozího vzorce, tedy
. Toto dosadíme do předchozího vzorce, tedy  . Zderivujeme podle r a maximum nalezneme položením derivace rovné nule.
. Zderivujeme podle r a maximum nalezneme položením derivace rovné nule.
Offline
#3 21. 05. 2008 23:13
- Slabsí matematik
- Příspěvky: 29
- Reputace: 0
Re: Slovni uloha - rotacni kuzel, rotacni valec
Ahoj Oline,
prosim te chtela bych se zeptat. Pokud zderivuji rovnici kterou uvadis podle r (zkousela jsem to,ale nevim, zda to delam spravne), zustane mi tam vice ruznych promenych, kdyz potom zderivovanou rovnici polozim nule, jak zjistim to maximum? Kdyz se me ptaji na rotacní válec, který má nejvetsi obsah pláste (bez podstav) co vlastne ode me chteji za udaj(vysledek)? rozmery toho valce, nebo hodnotu obsahu? nejak se v tom ztracim:-(
dekuji za pomoc
Offline
#4 01. 06. 2008 20:39
- Slabsí matematik
- Příspěvky: 29
- Reputace: 0
Re: Slovni uloha - rotacni kuzel, rotacni valec
Ahoj muze mi prosim nekdo poradit.
Zderivovala jsem S=2pihr((1- (r/R)) tak jak uvedl Olin podle maleho r a vyslo mi toto: 2pih-(4pihr/R)=0 ale co ted mam presne hledat, jakou promenou osamostatnit? h?
pokud ano pote mi vyjde: 2pi*(hR-2hr)=0 vydelim celou rovnici 2pi
hR-2hr = 0
h*(R-2r)=0 kdyz ted vydelim h tak o nej prijdu, jaky je tedy prosim postup a k cemu mam vlastne dojit, co ma byt vlastne odpovedi na otazku ( Do rotacniho kuzele o polomeru podstavy R a výsce h vepiste rotacní válec, který má nejvetsi obsah pláste (bez podstav)?
diky moc za pomoc
Offline
#6 01. 06. 2008 20:54
- Slabsí matematik
- Příspěvky: 29
- Reputace: 0
Re: Slovni uloha - rotacni kuzel, rotacni valec
ahoj, tak pokud muzu pokracovat v me rovnici, tak tedy: h*(R-2r)=0 vydelim h
R=2r
R/2 = r a to je tedy vse? nebo musim jeste nekam dosadit a neco pocitat a odpovet na otazku? diky
Offline
#7 01. 06. 2008 20:58
Re: Slovni uloha - rotacni kuzel, rotacni valec
teoreticky by se melo overit, jestli pro r = R/2 nastava maximum, ale v tomto pripade je zrejme, ze tomu tak skutecne je. takze jeste dopocitat vysku vepisovaneho valce z rovnice 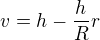 a dat dohromady slovni odpoved.
a dat dohromady slovni odpoved.
Offline
#8 01. 06. 2008 21:06
- Slabsí matematik
- Příspěvky: 29
- Reputace: 0
Re: Slovni uloha - rotacni kuzel, rotacni valec
takze tedy ted dosadim za male r =R/2
mam tedy v= h-h/R * (R/2)
v = h/2
jak bych to jeste mela overit to maximum? a nejsem si jista co presne chteji slyset v odpovedi....
Offline
#9 01. 06. 2008 21:14
Re: Slovni uloha - rotacni kuzel, rotacni valec
v odpovedi chteji nejspise slyset parametry vepisovaneho valce, takze polomer a vysku v zavislosti na polomeru a vysce kuzele. maximum by se overilo pomoci znamenka druhe derivace, ale tady to neni treba, je zrejme, ze je to maximum, minimum by bylo pro r = 0.
Offline
#10 01. 06. 2008 21:31
- Slabsí matematik
- Příspěvky: 29
- Reputace: 0
Re: Slovni uloha - rotacni kuzel, rotacni valec
ok dekuji moc za tvoji radu a pomoc
Offline
#11 30. 08. 2010 15:41 — Editoval clandestino (30. 08. 2010 15:42)
- clandestino
- Zelenáč
- Příspěvky: 3
- Reputace: 0
Re: Slovni uloha - rotacni kuzel, rotacni valec
Mám podobný problém. Ve válci mám rotační kužel, podstavu mají společnou, vrchol kužele je ve středu horní podstavy válce. Mám zadaný povrch válce a = 7,2 a povrch kužele b = 4,9. Z toho mám zjistit úhel, který svírá osa kužele s jeho povrchem. Zaboha ale nemůžu nějak rozumně vyjádřit r...
Offline
#12 30. 08. 2010 18:34
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovni uloha - rotacni kuzel, rotacni valec
↑ clandestino:
Zdravím,
myslím, že problém máš jiný - válec a kužel maji společnou podstavu (stejné R) a společnou výšku (v).
Výška se dá vyjádřit přes R a poloviční úhel u vrcholu (v trojuhelníku - řezu kuželu). Také se dá vyjádřit "boční strana" kuželu = poloměr rozbalené kruhové výseče).
K řešení bude soustava 2 rovnic 2 neznamé (poloměr R a úhel v řezu kuželu).
To je jen nástin - založ si prosím samostatné téma, toto téma je vyřešené. Děkuji.
Offline
#13 31. 08. 2010 14:19 — Editoval Cheop (31. 08. 2010 16:36)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Slovni uloha - rotacni kuzel, rotacni valec
↑ clandestino:
Tady je námět
http://www.ulozto.cz/5720153/valec-a-kuzel.html
PS: Obrázek je v poměru 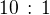
Edit
Nikdo není dokonalý
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Slovni uloha - rotacni kuzel, rotacni valec (TOTO TÉMA JE VYŘEŠENÉ)
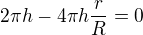 a z teto rovnice musime vyjadrit MALE r, vzdyt jsme podle nej diferencovali. zkus to upravit a vypocitat, vyjde to hezky. kdyztak se ozvi.
a z teto rovnice musime vyjadrit MALE r, vzdyt jsme podle nej diferencovali. zkus to upravit a vypocitat, vyjde to hezky. kdyztak se ozvi. kde
kde  je povrch válce a
je povrch válce a  je povrch kužele
je povrch kužele