Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 04. 2011 08:23
Linita ošklivé funkce
Dobrý den, dostal jsem za úkol vyřešit průběh funkce  Zaseknul jsem se na výpočtu limit spojitosti funkce. Vypočítal jsem si limitu v plus a míus nekonečnu a teď chci vypočítat limitu v bodech nespojitosti finkce tj.
Zaseknul jsem se na výpočtu limit spojitosti funkce. Vypočítal jsem si limitu v plus a míus nekonečnu a teď chci vypočítat limitu v bodech nespojitosti finkce tj. 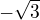 a
a 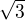 Přišel jsem na to že se to počítá přes jednostrané limity. Ale já nějak nevím jak na to. Mohli by jste mi podarit? Díky
Přišel jsem na to že se to počítá přes jednostrané limity. Ale já nějak nevím jak na to. Mohli by jste mi podarit? Díky
Offline
#2 29. 04. 2011 08:33
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Linita ošklivé funkce
Tak čitatel bude na okolí docela daleko od nuly, tam nás bude zajímat jen znaménko. Jmenovatel je zajímavější.
V zásadě ti mohu nabídnout tři postupy, ani jeden není příliš rigorózní. Jedno mají společné: limita jmenovatele je určitě nula, takže jednostranná limita zlomku bude vždy + nebo - nekonečno. Teď jak zjistit, které z toho:
1) Když zkoumáš hodnoty 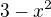 na okolí
na okolí  , tak vidíš, že pro hodnoty větší než
, tak vidíš, že pro hodnoty větší než  (jdeš tedy zprava) se dostáváš do mínusu a ve jmenovateli vytváříš nekonečně malé záporné hodnoty. Navíc čitatel bude kladný, takže limita zde bude minus nekonečno. Analogicky můžeš postupovat pro limitu zleva.
(jdeš tedy zprava) se dostáváš do mínusu a ve jmenovateli vytváříš nekonečně malé záporné hodnoty. Navíc čitatel bude kladný, takže limita zde bude minus nekonečno. Analogicky můžeš postupovat pro limitu zleva.
2) Můžeš si nakreslit parabolu 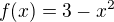 a ty hodnoty tam uvidíš hned.
a ty hodnoty tam uvidíš hned.
3) Můžeš si to rozložit podle vzorce  a stačí si pak nakreslit jen graf lineární funkce.
a stačí si pak nakreslit jen graf lineární funkce.
Pomohlo?
Offline
#3 29. 04. 2011 09:06 — Editoval pokus123 (29. 04. 2011 09:41)
Re: Linita ošklivé funkce
↑ halogan: MOžná pomohlo vypočítal jsem toto: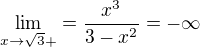



Limity v krajních bodech definičního oboru jsem počítal pomocí Lhospitalova pravidal to by mohlo být ne?? Ještě jsem se chtěl zeptat, pokud je to správně tak jak to mám zapsat do toho projektu?? Mám to tam napsat pčesně tak jak je to mám tady, nebo se to dá ještě nějak upravit?? Díky
Offline
#4 29. 04. 2011 09:36
#6 29. 04. 2011 09:55
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Linita ošklivé funkce
↑ pokus123:
L'Hospitalovým pravidlem? Kolik vyšlo?
Jde to pouhým pohledem, případně zjednodušením
Offline
#7 29. 04. 2011 10:35
Re: Linita ošklivé funkce
↑ halogan: Lhospitalovám pravidel m vyšlo  Obdobně pro mínus nekonečno
Obdobně pro mínus nekonečno
Offline
#8 29. 04. 2011 10:52
Re: Linita ošklivé funkce
↑ halogan:To my vysvětli kde v tom druhém zlomku se to ztratla ta trojka a dále pak když máš X/-X to je plus nekonečno děleno mínus nekonečnem a mám takocý pocit že to tak nějak není definováno
Offline
#9 29. 04. 2011 10:58
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Linita ošklivé funkce
↑ pokus123:
Ono to není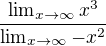 ,
,
ale jen 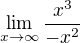 , takže nedělím žádná nekonečna, jen proměnné x. Tolik k druhému dotazu.
, takže nedělím žádná nekonečna, jen proměnné x. Tolik k druhému dotazu.
K tomu prvnímu: Když jdeme s x to nekonečna, ta trojka tam hraje stále menší a menší roli. Přeci jen rozdíl mezi 1000^3/(3-1000^2) a - 1000 není tak velký.
Proto jsem i říkal, že není potřeba L'Hospitalovo pravidlo (ani dle mého není vítáno, protože je nutné zkontrolovat, že naše limita vyhovuje jeho podmínkám!), protože naše funkce je "zhruba" -x.
Offline
#10 29. 04. 2011 11:04
#13 01. 05. 2011 13:42
Re: Linita ošklivé funkce
↑ halogan: a kam se tedy ztratila ta trojka?
děkuji
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#14 01. 05. 2011 13:45
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Linita ošklivé funkce
↑ byk7:
Intuitivně: Ta trojka tam nemá skoro žádný vliv, zvlášť pro velká x.
Matematicky: Rozšiř to výrazem x^2/x^2 a rozděl na součin dvou limit. Zbyde tam to moje a jedna limita, která vyjde 1.
Offline
#15 01. 05. 2011 14:18
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Linita ošklivé funkce
↑ byk7:
formálně vzato vytkneš x^2 ve jmenovateli, z trojky ti zbude 3/x^2, pak vykrátíš x^2, pak použiješ tu aritmetiku limit, výraz nahoře je x a ten má limitu nekonečno, výraz dole je -1+(3/x^2) a to má limitu -1
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#16 01. 05. 2011 14:52
Re: Linita ošklivé funkce
↑ OiBobik:↑ OiBobik:↑ OiBobik: Tak jsou ty výše uvedené limity dobře nebo ne??
Offline
#17 01. 05. 2011 15:24
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Linita ošklivé funkce
↑ pokus123:
Jsou, vždyť i ten tvůj L'Hospital je správný postup, já jen odpovídal ↑ byk7: na jeho dotaz, jak formálně správně to odvodit bez L'Hospitala, tedy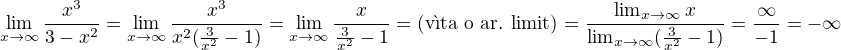
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline