Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 05. 2011 01:44
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Parciální derivace integrálu
Zdravím všechny.
Chtěl bych poprosit o radu s následujícím příkladem: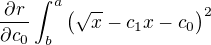
Nemůžu přijít vůbec na žádný způsob jak to spočítat. Když by tam ještě byla suma, tak bych tu dvojku asi jenom hodil před to, ale když je tam ten integrál, tak moc nevím co si " můžu dovolit ".
Vím, že někde existovaly věty o záměně derivace a integrálu, ale to bylo spíš u nějakých řad, tak já nevím.
Díky za odpověď.
Offline
#2 09. 05. 2011 10:40 — Editoval Rumburak (09. 05. 2011 10:44)
Re: Parciální derivace integrálu
↑ ondrej.hav:
Věta o derivaci integrálu podle parametru je vyslovena zde (množinou M bude v Tvé úloze interval [b, a] ).
Ale v tomto případě klidně můžeme pořadí akcí dodržet - nejdříve spočítat daný integrál (neboť to umíme) a zderivovat až výsledek integrace.
Offline
#3 09. 05. 2011 14:22
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Parciální derivace integrálu
↑ Rumburak:
Tak nevím, ale podle me ten integrál neupočítám... Mohl by si mi poradit jak na něj?
Offline
#4 09. 05. 2011 14:37 — Editoval ondrej.hav (09. 05. 2011 14:39)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Parciální derivace integrálu
↑ Rumburak:
Pokud bych pořadí operací zaměnil, tak bych dostal  A to bych upravil na
A to bych upravil na 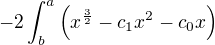 a to by bylo
a to by bylo ![kopírovat do textarea $ \left[ \frac25 x^\frac52 -c_1 \frac{x^3}{3} - c_0 \frac{x^2}{2}\right]_{a}^{b}$](/mathtex/20/203ac625a48c688740173ed7f4c1fa49.gif)
Je to tak? Díky
P.S.: Pokud bych měl integrovat i stou mocninou, tak mi to porad nejak nejde...
Offline
#5 09. 05. 2011 14:38 — Editoval Rumburak (09. 05. 2011 15:37)
Re: Parciální derivace integrálu
↑ ondrej.hav:
Začni tím, že umocníš tu závorku . Integrand pak bude součtem členů tvaru 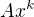 , (kde A, k jsou konstanty, k >= 0),
, (kde A, k jsou konstanty, k >= 0),
což se integruje poměrně snadno (použije se též linearita integrálu).
Offline
#6 09. 05. 2011 14:42
Re: Parciální derivace integrálu
↑ ondrej.hav:
Místo podle c_0 jsi to ale zderivoval podle c_1 .
Součástí tohoto postupu je též ověřit, že jsou splněny předpoklady příslušné věty.
Offline