Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » L'Hospitalovo pravidlo (TOTO TÉMA JE VYŘEŠENÉ)
#2 12. 05. 2011 08:43
Re: L'Hospitalovo pravidlo
Zdravím, tento příklad se tu už jednou počítal, je třeba hledat, výsledek je 
to si pamatuju, bylo to tu celkem nedávno , nemám čas tedka to rezepisovat, zkus hledat kdyžtak.
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#3 12. 05. 2011 09:33
#4 12. 05. 2011 22:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: L'Hospitalovo pravidlo
↑ urnacka:
Zdravím,
nějak to zapadlo. Pokud jsem správně pochopila zápis, potom pro použití l´Hospital pravidla jsem přepsala na "oo"/"oo":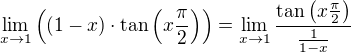
potom jsem 3x použila l´Hospital pravidlo.
Pro jistotu zkontroluj zleva a zprava od 1, zda vychází stejně (mně vyšlo, ale bez záruky)
Snad pomůže, případně se ozvi.
------------
EDIT: l´Hospital byl 3x.
Offline
#6 12. 05. 2011 22:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: L'Hospitalovo pravidlo
↑ urnacka:
pro čitatel chybí derivace vnitřní funkce, pro jmenovatel derivace 
V pořádku?
Offline
#7 12. 05. 2011 22:39
Re: L'Hospitalovo pravidlo
↑ jelena:
áha jo uz to vidím toho jmenovatele jsem dala pekne blbe jak koukam
ja si moc nevim rady s tim citatelem s jak bych ho jinak mela zderivovat
a kdyz zderivuju po druhé jmenovatele
tak mi vyjde 2*(1-x)^-3 takze mi porad vychazi 0 nevim si uz rady, jsem asi natvrdla
Offline
#8 12. 05. 2011 22:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: L'Hospitalovo pravidlo
po 1. l´Hospital vychází: 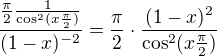
Zvládneš to dál?
--------------------------- EDIT-------------------------------------
Po 2. l´Hospital 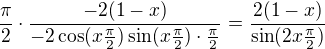
a po 3. l Hospital>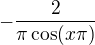
zde jsem dosazovala x=1.
Offline
#10 13. 05. 2011 08:14 — Editoval maly_kaja_hajnejch-Lazov (13. 05. 2011 08:15)
- maly_kaja_hajnejch-Lazov
- Příspěvky: 467
- Reputace: 24
Re: L'Hospitalovo pravidlo
Ja bych rozdelil tangens a sinus lomeno kosinus, ten sinus dal zvlast (limita je jedna) a pocital limitu jenom z toho, co zbyde.
viz http://user.mendelu.cz/marik/lhosp.pdf priklad 34 a 34B
Offline
#11 13. 05. 2011 08:37
#12 13. 05. 2011 09:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: L'Hospitalovo pravidlo
↑ maly_kaja_hajnejch-Lazov:
Děkuji a zdravím Vás :-)
Jednou se vzchopím, že něco vypočtu, protože Wolfram postup nenabízel, jenže už neumím tabulku goniometrických funkcí - při tomto přepisu zadání mi vyšlo (0*0)/1 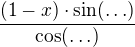
Tak jsem tuto cestu zavrhla a šla jsem z Opavy na Politaví přes Oděssu. Koná se tento rok tradiční odstřel?
↑ urnacka:
Omlouvám za zbytečnou složitost, přidám, až budu mít čas, svého posledního l´Hospital, ale je to opravdu cesta zbytečná a nepěkná, přímo ošklivá.
Věnuj prosím trochu více pozornosti derivaci složených funkci (jsou v tom chyby), ale po tom svém výkonu nemám nárok něco doporučovat. Doufám, že mou omluvu příjmeš, děkuji.
Offline
#13 13. 05. 2011 13:40
- maly_kaja_hajnejch-Lazov
- Příspěvky: 467
- Reputace: 24
Re: L'Hospitalovo pravidlo
↑ jelena:
Pekny den, obdiv Vasi neustale aktivite a ochote radit. Ja ted forum trosku dlouhodobe zanedbavam :)
O babickem strileni zatim nevim, ani zadna mista pro nahradu odstrelenych kusu vypsana nejsou. Minule tri odstrelene kusy byly s uspechem nahrazeny jednim mladym kusem. Hospodari rikali, ze to musi stacit :)
Offline
#15 14. 05. 2011 09:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: L'Hospitalovo pravidlo
↑ urnacka:
také děkuji, už jsem svou trnitou cestu doeditovala ↑ jelena: (je alespoň vidět, jak jsem statečně obešla výpadek hodnot goniometrických funkcí pro pi/2 a použila jsem hodnotu, kterou jsem si pamatovala.
↑ maly_kaja_hajnejch-Lazov:
:-) děkuji, tomu se neříká "aktivita", ale jinak.
OT: jak jsem pozorně četla Karolínu, tak její hlavní účel byl vybudovat si podmínky, aby mohla si v klidu a nerušeně číst. Že z toho nabudovali spolků a navěsili na ni různé povinnosti, byla celkem rozhořčená a otrávená (poptejte se odborníků).
Mějte se hezky a děkuji velmi za příspěvky.
Jelena.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » L'Hospitalovo pravidlo (TOTO TÉMA JE VYŘEŠENÉ)
 \lim_{x\to1}[(1-x) tan xPi/2}
\lim_{x\to1}[(1-x) tan xPi/2}