Matematické Fórum

FliegenderZirkus · 22. 05. 2011 10:58

Ahoj, mám jeden problém související se známou substitucí za tangens polovičního úhlu v integrálním počtu. Uvažujme čtvrtinu elipsy
$x&=a \cos t \\ y&=b \sin t \ , \ t \in \left[0,\frac{\pi}{2}\right]$
Když použijeme substituci 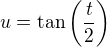$u=\tan\left(\frac{t}{2}\right)$ , tak „racionalizujeme“ tuto parametrizaci na
$x&=a \frac{1-u^2}{1+u^2} \\ y&=b \frac{2u}{1+u^2} \ , \ u \in \left[0,1\right]$

Tento postup funguje vždy, když jsou souřadnicové funkce nějaké funce sinů a cosinů, alespoň tedy na nějakém intervalu. Zkoušel jsem ale podobně „racionalizovat“ obyčejnou sinusoidu
$x&= t \\ y&=\sin t \ , \ t \in \left[0,2\pi\right]$
a myslím, že to nejde. Jak by se dalo o nějaké křivce dokázat, že neexistuje její racionální parametrizace? A kdybychom všechny křivky (v rovině nebo v prostoru) rozdělili na ty, které „racionalizovat“ jdou a na ty, které nikoli, jak by vypadaly tyto množiny? Tento problém má velmi reálnou aplikaci v počítačové grafice...

musixx · 24. 05. 2011 13:34 — Editoval musixx (24. 05. 2011 13:54)

Byl jsem tady přes 'Soukromé zprávy' (o nichž jsem do dneška netušil, že existují) požádán, abych se k tomuto vyjádřil. Třeba mě doplní některý u místních analytiků (já raději algebru).

Celá otázka tak ani není o substituci v integrování, jako spíš o "racionalizaci", kde ovšem nelinearita, nepolynomiálnost, atd. je schována v substituci (něco jako třeba logaritmické měřítko na ose x při vykreslování grafů).

Obecně se líbí, když se objevují tzv. racionální lomené funkce, tedy v podstatě podíl dvou polynomů nějaké proměnné.

V dalším se nebudu trápit definičními obory atd. Ono by to plynulo z podrobnějšího rozboru. Pišme tedy dále více populárně...

Vezmeme-li jakékoli parametrické vyjádření křivky v rovině, tedy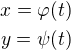
$x=\varphi(t)\\y=\psi(t)$ ,
uvážíme-li substituci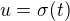
$u=\sigma(t)$
a chceme-li po této substituci mít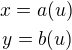
$x=a(u)\\y=b(u)$
(ať už klademe jakékoli požadavky na funkce a a b -- třeba že jsou racionální lomené), pak přeci nutně musí být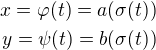
$x=\varphi(t)=a(\sigma(t))\\y=\psi(t)=b(\sigma(t))$ ,
kde z první rovnosti máme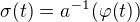
$\sigma(t)=a^{-1}(\varphi(t))$
a z druhé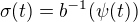
$\sigma(t)=b^{-1}(\psi(t))$ ,
proto také například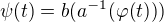
$\psi(t)=b(a^{-1}(\varphi(t)))$ .

Proto příklad s elipsou "vyšel" -- po a a b totiž chceme, aby byly racionální lomené, tedy v jejich inverzích se objeví tak maximálně odmocniny a vztah mezi sinem a kosinem lze takto udělat (jedna mínus sinus na druhou je kosinus na druhou). A proto také druhý uvedený příklad nemá naději na úspěch, protože z lineární funkce se na sinusoidu jen pomocí mocnin a odmocnin a ostatních "obvyklostí" v konečném procesu přejít nedá (kdyby to šlo, pak $\pi$ je algebraické, ale to není).

Do obecné klasifikace se ale raději pouštět nebudu. Tam by bylo třeba o hodně víc přidat na opatrnosti v soudech, protože i jen spojité křivky v rovině umí být hezky záludné.

FliegenderZirkus · 28. 05. 2011 20:42

↑ musixx:

Díky za reakci. S tou intervencí nemám nic společného, o soukromých zprávách také slyším poprvé.

Cesta k nějakým obecnějším a formálnějším závěrům by tedy pravděpodobně vedla přes vlastnosti inverzních funkcí k funkcím racionálním lomeným...do čehož se pouštět určitě nebudu. Tohle objasnění mi stačí. Kdybych chtěl vymodelovat kus sinusoidy jako NURBS, tak bych pravděpodobně napočítal několik bodů a ty interpoloval. Nebo by asi šlo nahradit ji Taylorovým polynomem, který už můžu vymodelovat jednoduše. Takže označuju jako vyřešené, díky!

Matematické Fórum

#1 22. 05. 2011 10:58

Univerzální goniometrická substituce

#2 24. 05. 2011 13:34 — Editoval musixx (24. 05. 2011 13:54)

Re: Univerzální goniometrická substituce

#3 28. 05. 2011 20:42

Re: Univerzální goniometrická substituce

Zápatí