Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 05. 2011 17:30
Dokažte (integrály, řady, konvergence)
Ahoj, moc moc prosím o radu jak se dokazují následující dvě tvrzení... díky.. nějak se v tom plácám
-když má funkce v nekonečnu konečnou limitu, musí tam mít její derivace limitu nulovou
- funkce stejnoměrně spojitá, integrál od nuly do nekonečna konverguje, dokázat že limita v nekonečnu musí být nula..
diky moc
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#3 26. 05. 2011 17:47
Re: Dokažte (integrály, řady, konvergence)
Mohl bys, prosím, své úvahy rozvést?
podle knihy by měly platit obě - z čeho soudíš, že to neplatí?
ad druhé tvrzení. Já se pokoušela následujícím zpúsobem: napsala jsem si definici stejnomerne spojitosti a pak predpokladala:¨
1)integral konverguje tzn pro kazde epsilon kladne existuje c (c z intervalu (0, infty), ze pro kazde x,x_1 z intervalu (c,infty) plati ze abs. hodnota z integralu v techto mezich je mensi nez epsilon
2)ze limita f v nekonecnu se nerovna nule tzn abs(f(x))>delta
a chci dojit ke sporu
z toho mam do stejnomerne spojitosti nejake abs( f(x) - f(x_1) )<epsilon_1
abs( delta - f(x_1) )<epsilon_1 .... dal jsem se nedostala....
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#4 26. 05. 2011 18:07 Příspěvek uživatele halogan byl skryt uživatelem Stýv. Důvod: i ty, brute?
#5 26. 05. 2011 18:08
Re: Dokažte (integrály, řady, konvergence)
tak se napřed podíváme na to první tvrzení. podívej se na graf:
tady se můžeš inspirovat. chce to najít nějakou funkci, která bude hladká (i když v předpokladech to neni explicitně zmíněno, ale jinak by to bylo triviální), její "zuby" se budou snižovat (aby existovala limity), ale současně se budou zkracovat, takže budou pořád dost "strmý" (aby derivce neměla limitu)
schválně neuvádím konkrétní protipříklad, na ten musíš přijít sama
když jse mto tak sepsal, tak mě napadá, že za předpokladu, že limita tý derivace existuje, by to asi platilo
Offline
#6 26. 05. 2011 18:19
Re: Dokažte (integrály, řady, konvergence)
↑ Stýv:
To se mi zdá jako velmi dobrý protipříklad, děkuji.
Je tedy možné, že k tomu byl přidán předpoklad existence derivace. Nečtu to z knihy, ale mám to z druhé ruky typu "co jsem dostal na zkoušce, nevyřešil, ale má to vyjít":-)
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#7 26. 05. 2011 18:27
Re: Dokažte (integrály, řady, konvergence)
↑ Esperance: tak pokud by ta derivace měla limitu, ale nenulovou, (búno kladnou) tak tu funkci snadno zespoda omezíš nějakou přímkou, která jde k nekonečnu
Offline
#8 26. 05. 2011 19:46
Re: Dokažte (integrály, řady, konvergence)
Chápu, děkuji.
Mohl bys mi prosím ještě osvětlit jak pokračovat (nebo se vydat uplně jinou cestou) u tvrzení 2?
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#11 26. 05. 2011 20:53
Re: Dokažte (integrály, řady, konvergence)
↑ Esperance: to určitě ne. třeba sin(x) nemá limitu 0 a přitom sin(x)=0 pro některý x z libovolnýho okolí nekonečna
Offline
#12 26. 05. 2011 21:07 — Editoval Pavel Brožek (26. 05. 2011 21:08)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dokažte (integrály, řady, konvergence)
↑ Esperance:
Podle mě musíme i v druhém tvrzení předpokládat, že limita v nekonečnu existuje, jinak to neplatí.
(Pokud bude zájem, pokusím se zkonstruovat protipříklad.)
Offline
#14 26. 05. 2011 21:13
Re: Dokažte (integrály, řady, konvergence)
↑ Stýv:
já teď moc nechápu tu analogii. Sinus na celem svem Df nemá limitu, protože osciluje... na vybraných monotonich intervalech prosim... ale nevím jak mi to má pomoct?
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#15 26. 05. 2011 21:15
#16 26. 05. 2011 21:21
Re: Dokažte (integrály, řady, konvergence)
↑ Esperance: ty jsi vlastně napsala
limita f v nekonecnu se nerovna nule tzn abs(f(x))>delta kazda x z df průnik okolí nekonecna
já ti ukázal příklad funkce, pro kterou tvoje tvrzení neplatí. jenom chci, aby sis rozmyslela, jak je to s tím abs(f(x))>delta: pro jaká x? pro jaká delta to platí? (nebo spíš pro kolik x, delta to platí?)
Offline
#17 26. 05. 2011 21:42
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dokažte (integrály, řady, konvergence)
↑ Stýv:
Asi máš pravdu, nerozmyslel jsem si to dost podrobně. Je tam podstatná ta stejnoměrná spojitost.
Offline
#18 26. 05. 2011 21:43
Re: Dokažte (integrály, řady, konvergence)
no tak co mě napadá:
zápis, že limita je nula
pro každé delta větší než nula existuje okolí nekonečna takové, že pro každé x z Df průnik okolí nekonečna (kromě nekonečna), x patčí do okolí_nek. => abs(f(x))<delta
negace
existuje delta vetsi nez nula, ze pro kazde okoli nekonecna..... x patri do okoli a abs(f(x))>delta.
takze to plati jen pro nejaka delta a pak to x patri do okoli...
no nejak z toho nejsem moudrá
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#19 26. 05. 2011 22:06
Re: Dokažte (integrály, řady, konvergence)
↑ Esperance: to už je lepší. búno navíc můžeme předpokládat, že přímo  pro nějaký
pro nějaký  na libovolnym okolí
na libovolnym okolí  . takže si vezmeš nějaký takový
. takže si vezmeš nějaký takový  a
a  , a z tý stejnoměrný spojitosti ukážeš, že
, a z tý stejnoměrný spojitosti ukážeš, že  dokonce na nějakym
dokonce na nějakym 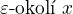 . pak si vezmeš další
. pak si vezmeš další  za timhle okolíčkem a uděláš to samý atd. takže máš nekonečnou posloupnost obdélníčků
za timhle okolíčkem a uděláš to samý atd. takže máš nekonečnou posloupnost obdélníčků 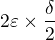 ...
...
Offline
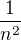 a výšce 1.
a výšce 1.