Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » nelinearna diferencialna rovnica asi (TOTO TÉMA JE VYŘEŠENÉ)
#4 26. 05. 2011 14:24 — Editoval Rumburak (26. 05. 2011 14:25)
Re: nelinearna diferencialna rovnica asi
↑ vysoka:
2y'y'' znamená 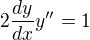 a ne to, co jsi napsal(a) Ty.
a ne to, co jsi napsal(a) Ty.
Nebo zkus rovnici 2y'y''=1 integrovat přímo - tak, jak je. Na první pohled je vidět, čeho je její levá strana derivací.
Offline
#5 26. 05. 2011 14:37 — Editoval vysoka (26. 05. 2011 14:44)
Re: nelinearna diferencialna rovnica asi
↑ Rumburak:myslal som to tak, napisal inak ... ospravedlnujem sa za preklep
ale vsak je to dobre zintegrovane ?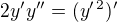 toto je yintegrovana lava strana ,ze ?
toto je yintegrovana lava strana ,ze ?
Offline
#8 26. 05. 2011 15:02 — Editoval Rumburak (26. 05. 2011 15:04)
Re: nelinearna diferencialna rovnica asi
Offline
#13 27. 05. 2011 09:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: nelinearna diferencialna rovnica asi
↑ vysoka:
Zdravím,
také mi to tak vyšlo. Myslím, že to je "obecné řešení" (na úvod tématu nemáš uvedeno nic upřesňujcícho, jaké řešení hledáš, vůbec toho v úvodním příspěvku moc není).
Překontrolovat můžeš derivováním svého výsledku a sestavením původní rovnice, např. (nebo ve Wolfram).
Offline
#14 27. 05. 2011 10:11
Re: nelinearna diferencialna rovnica asi
↑ jelena:wolfram som spomenul hned na zaciatku :) no bol by som rad - ak sa este daju najst aj dalsie riesenia , len opat to asi pojde len s vaou pomoci .... idem na vysetrenie tak asi pridem az popoludni .... diky vsem
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » nelinearna diferencialna rovnica asi (TOTO TÉMA JE VYŘEŠENÉ)

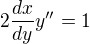 takto ?
takto ?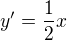 ?
?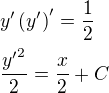
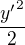 to je myslene ypsilon derivovane a na druhu ?
to je myslene ypsilon derivovane a na druhu ? 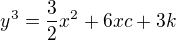 ?
?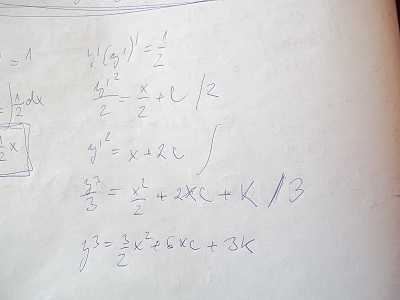
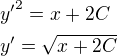 a teraz obe strany zintegruj
a teraz obe strany zintegruj 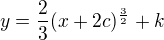 ?? hotovo :) ci toto je len vseobecne riesenie ? dik za trpezlivost
?? hotovo :) ci toto je len vseobecne riesenie ? dik za trpezlivost