Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » slovní úloha - použitím metody integračního faktoru (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 05. 2011 20:48
slovní úloha - použitím metody integračního faktoru
ahoj, mám tu krapet problém s touhle slovní úlohou
Současná cena domu je 200 000 EUR. Přepokládejme odhad, že po t měsících bude cena p(t) růst rychlostí
p´(t)=0.01 p(t)+1000t EUR měsíčně. Kolik bude dům stát za 9 měsíců? má se použít metoda integračního faktoru...
nějak nevim, jak začít ...
Offline
- (téma jako vyřešené označil(a) jelena)
#2 28. 05. 2011 22:01
Re: slovní úloha - použitím metody integračního faktoru
tak začni asi tím, že si dáš polynom s koeficientem 0,01 na levou stranu a popřemýšlíš jak "schovat celou levou stranu pod derivaci"
http://en.wikipedia.org/wiki/Integrating_factor tady je trochu teorie, pokud to nemáš někde u sebe
Offline
#3 29. 05. 2011 00:14 — Editoval Geronimo (29. 05. 2011 13:15)
Re: slovní úloha - použitím metody integračního faktoru
Převedeš p(t) na levou stranu.
Podíváš se, jaký koeficient (nazveme jej a) je u p(t) (i se znamenkem) a celou rovnici pronasobis 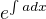
Potom hledas na leve strane puvodni derivaci, vetsinou to jde videt na prvni pohled a byva to derivace ze soucinu promenne a integracniho faktoru.
Potom staci integrovat a vyjadrit hledanou promennou.
„Jestliže neumíš – naučíme, jestliže nemůžeš – pomůžeme ti, jestliže nechceš – nepotřebujeme tě.“ —Jan Werich
Offline
#5 29. 05. 2011 13:14
Re: slovní úloha - použitím metody integračního faktoru
↑ 007Misak:
Já zas neumím poznavat stranu...
Figl je v tom, ze vsechny cleny s promenou budes mit na jedne strane a vsechno ostatni na druhe. Potom pronasobis tim integracnim faktorem...
„Jestliže neumíš – naučíme, jestliže nemůžeš – pomůžeme ti, jestliže nechceš – nepotřebujeme tě.“ —Jan Werich
Offline
#7 10. 05. 2012 21:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovní úloha - použitím metody integračního faktoru
↑ pepiik:
Zdravím,
rovnici upravím na p´(t)-0.01 p(t)=1000t, odsud a=-0.01 a můžeš pokračovat dle doporučení kolegů a např. dle tohoto materiálu. Už se podaří? Děkuji.
Offline
#9 10. 05. 2012 23:43
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovní úloha - použitím metody integračního faktoru
↑ pepiik:
celkem dobře, pokud zintegruješ exponent 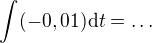 , tak to nebude vypadat tak strašně.
, tak to nebude vypadat tak strašně.
Jen bych opravila znaménko v exponentu na úvod - má být ještě "minus" (ale raději si to překontroluj, těch minusů je moc :-)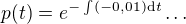
Offline
#10 12. 05. 2012 22:57 — Editoval pepiik (12. 05. 2012 22:59)
Re: slovní úloha - použitím metody integračního faktoru
ano měl jsem tam blbě to mínus nicméně dál jsem zase v koncích.
a to vím že výsledek v t=9 má vyjít 260 578 a dopočítat se nemohu.
zkoušel jsem rady příspevků nahoře pronásobit to tím faktorem. rovnici jsem pronásobil a tam jsem zase v koncích :D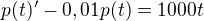
pronásobit rovnici faktorem :r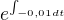
vyšlo 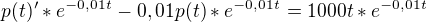
dál zase nevím :/
Offline
#11 12. 05. 2012 23:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovní úloha - použitím metody integračního faktoru
↑ pepiik:
po zintegrování 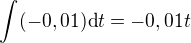 dosadím do:
dosadím do: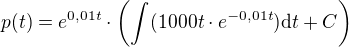
Až dointegruješ (per partes), tak potom C najít z podmínky, že pro t_0=0, p(t)=200000 a novou cenu dosazením t=9.
Offline
#14 13. 05. 2012 22:43
Re: slovní úloha - použitím metody integračního faktoru
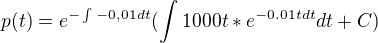
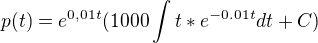
per partes :
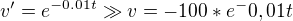
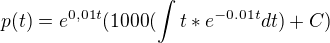
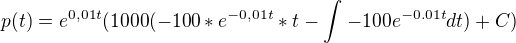
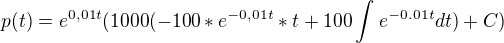
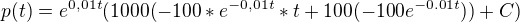
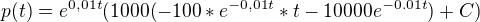
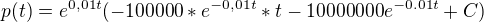
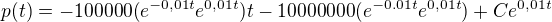
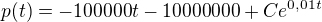
v p(0)=200000 >> C=10 200 000
vysledna : 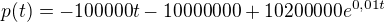
p(18)= 411 617,1 EUR
Děkuji moc Jelena za pomoc a trpělivost. byl to boj ale nakonec se povedlo :D
PS jak to označit jako vyřešené když nejsem tvůrce tématu ?
Offline
#15 14. 05. 2012 08:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovní úloha - použitím metody integračního faktoru
↑ pepiik:
děkuji za hlášení a za komplet řešení, potěšilo :-)
p(18)= 411 617,1 EUR
Původně jsi chtěl za 9 měsíců (jen pro upřesnění, zda má být 18)? I tak označuji za vyřešené.
Offline
#17 04. 06. 2013 22:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovní úloha - použitím metody integračního faktoru
↑ Fajfi:
V zadání - viz ↑ 1. příspěvek: je požadavek za 9 měsíců.
Kolik bude dům stát za 9 měsíců?
kolega chybně dosazoval 18 měsíců, ale princip je stejný (jen si zkontroluj zadání). Je všechno jasné? Děkuji.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » slovní úloha - použitím metody integračního faktoru (TOTO TÉMA JE VYŘEŠENÉ)

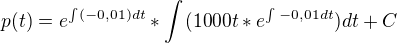
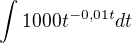 podle vzorce z toho materiálu by mělo být
podle vzorce z toho materiálu by mělo být