Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 06. 2011 10:19
Kovariance
Ahoj, mám zadanou následující tabulku:
Y|X 1 2 3
0 1/10 1/12 1/15
1 1/15 1/4 13/30
Mám z ní vypočítat korelaci corr(X,Y).
Pro corr platí vzorec: 
Pro cov(X,Y) platí: 
Dílčí pravděpodobnosti se spočítají: 
Nevím ale jak spočítát 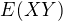 resp našel jsem vzorec, podle kterého to spočítat ale neumím ho aplikovat. Ten vzorec je takovýto:
resp našel jsem vzorec, podle kterého to spočítat ale neumím ho aplikovat. Ten vzorec je takovýto:  Mohl by mi někdo napsat, jakým způsobem tam dosadit hodnoty z tabulky ? Především jak naložit s tím členem
Mohl by mi někdo napsat, jakým způsobem tam dosadit hodnoty z tabulky ? Především jak naložit s tím členem 
Děkuji za pomoc.
Offline
- (téma jako vyřešené označil(a) Mathe)

