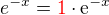Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » sustavva diferencialnych rovnic objasnenie rieseneho postupu (TOTO TÉMA JE VYŘEŠENÉ)
#2 19. 06. 2011 13:07
- maly_kaja_hajnejch-Lazov
- Příspěvky: 467
- Reputace: 24
Re: sustavva diferencialnych rovnic objasnenie rieseneho postupu
ten prvni oval: je tam preskocena spousta kroku, ale pocitam, ze nehomogenni diferencialni rovnice druheho radu umite resit.
ten druhy: dosadi se do rovnice, kdy je x_2 vyjadreno pomoci x_1 a x'_1
Offline
#3 19. 06. 2011 13:08 — Editoval Pavel Brožek (19. 06. 2011 13:09)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: sustavva diferencialnych rovnic objasnenie rieseneho postupu
↑ vysoka:
Převedli jsme soustavu dvou diferenciálních rovnic na jednu diferenciální rovnici. Tu už bys asi měl umět vyřešit, proto je v textu už jen uveden výsledek (první červeně vyznačený řádek). Tento výsledek je pak dosazen do rovnice 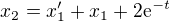 , abychom dostali řešení
, abychom dostali řešení  .
.
Edit: Můj příspěvek v podstatě říká to samé jako ↑ maly_kaja_hajnejch-Lazov:, jen jinými slovy, tak ho tu už nechám.
Offline
#4 19. 06. 2011 13:57 — Editoval vysoka (19. 06. 2011 13:58)
Re: sustavva diferencialnych rovnic objasnenie rieseneho postupu
↑ maly_kaja_hajnejch-Lazov:↑ Pavel Brožek: podaril osa mi vyriesit rovnicu bez pravej strany - cleny vysli 2 a 1
cize riesenie 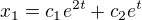 len neviem este ako doriesit tu rovnicu s tou pravou stranou ... aby sme sa dostali k pozadovanemu cervenemu prvemu ovalu.
len neviem este ako doriesit tu rovnicu s tou pravou stranou ... aby sme sa dostali k pozadovanemu cervenemu prvemu ovalu.
Offline
#6 19. 06. 2011 14:03 Příspěvek uživatele Pavel Brožek byl skryt uživatelem Pavel Brožek. Důvod: Už napsal jarrro
#7 19. 06. 2011 14:04 — Editoval vysoka (19. 06. 2011 14:05)
Re: sustavva diferencialnych rovnic objasnenie rieseneho postupu
↑ jarrro:ano , len jak an to ?↑ Pavel Brožek: dik...
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » sustavva diferencialnych rovnic objasnenie rieseneho postupu (TOTO TÉMA JE VYŘEŠENÉ)

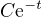
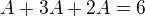 cize
cize  takze
takze  :(
:(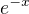 ani srnka netusi ........
ani srnka netusi ........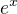 veď riešenie je tvaru
veď riešenie je tvaru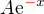 čo ťa viedlo k záveru,že je to
čo ťa viedlo k záveru,že je to