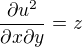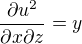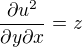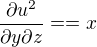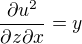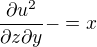Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » viazane extremy u=xyz (TOTO TÉMA JE VYŘEŠENÉ)
#5 04. 06. 2011 22:41 — Editoval Alivendes (04. 06. 2011 22:44)
Re: viazane extremy u=xyz
↑ vysoka:
:o) víš, jak se počítají parciální derivace ?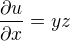
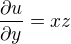
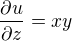
Derivujeme podle jednotlivé proměnné, všechno ostatní bereme jako konstanty..budeme ale potrebovat i druhé parciální derivace ...jaké budou?
Dále platí: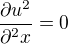
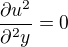
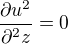
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#7 04. 06. 2011 22:56 — Editoval vysoka (04. 06. 2011 22:57)
Re: viazane extremy u=xyz
↑ Alivendes:
DAKUJEM ...
ano / parcialne derivacie viem / len vzsy treba peclivo sledovat podla coho a kolko premennych derivujeme ...
tie parcialne derivacie je vcelku hracka pri takychto vcelku jednoduchych dunkciach ... zlozitejsie je hladanie konkretnych bodov ... samotne parcialne derivacie nam nepomozu ak nevieme co mame s nimi robit
Offline
#10 04. 06. 2011 23:54 — Editoval Alivendes (05. 06. 2011 00:18)
Re: viazane extremy u=xyz
Determinant mi vyšel takto: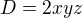
Náš stacionární bod:![kopírovat do textarea $a=[0,0,0]$](/mathtex/41/41608d46e7c92ed1f56db5c28777f354.gif)
Determinant ma pro bod a hodnotu 0, funkce má v bodě [0,0,0] sedlový bod.
Nicméně prosím o kontrolu, žádné extrémy nám nevyšly. Je to vidět ale i logicky, jedná se o součin 3 čísel a funkčni hodnota se bude pohybovat od minus nekonecna do nekonecna.
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#11 05. 06. 2011 00:18
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: viazane extremy u=xyz
↑ Alivendes:
Bohužel, způsobem, který popisuješ, zjistíš lokální extrémy jinde než na množině bodů zadaných vazbou.
Zde je asi potřeba postupovat pomocí Lagrangeových multiplikátorů.
Offline
#12 05. 06. 2011 00:20
Re: viazane extremy u=xyz
↑ Pavel Brožek:
Díky :)
Opravdu jsem si toho všiml až na konci, tak jsem to takto dopočítal.
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#13 05. 06. 2011 00:29
Re: viazane extremy u=xyz
↑ Pavel Brožek:
Nicméně to co navrhuješ jsem ještě nikdy nepočítal, a teď vnoci se to učit nebudu, dobrou noc a omlouvám se, že jsem počítal něco jiného.
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#14 05. 06. 2011 07:43
Re: viazane extremy u=xyz
↑ Alivendes:dik za kazdu pomoc :)
...boj so spankom bol u mna prehratz ale uz o 23>05 h ... takze vcera vecer uz bez mojej reakcie :(
Offline
#16 20. 06. 2011 11:35
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: viazane extremy u=xyz
↑ vysoka:
Ano, ta funkce F je správně.
Offline
#17 20. 06. 2011 11:39 — Editoval vysoka (20. 06. 2011 11:49)
Re: viazane extremy u=xyz
↑ Pavel Brožek:tak mozme derivovat ... :)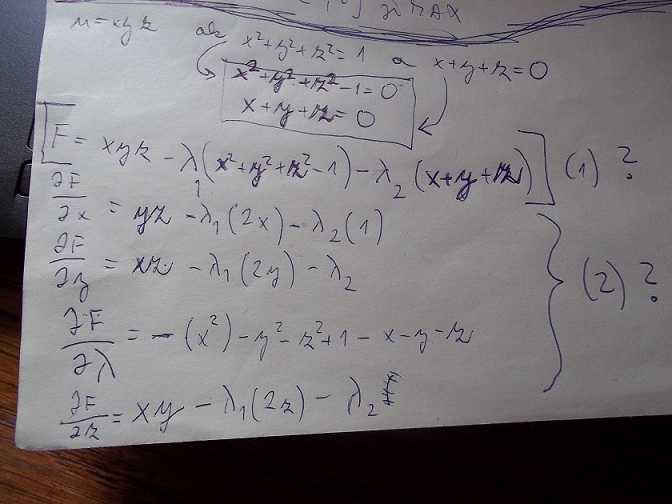
no a ako skoncil pAPIER , TA K AJ JA S NAPADMI AKO DALEJ :(...
Offline
#19 20. 06. 2011 22:24
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: viazane extremy u=xyz
↑ vysoka:
Multiplikátory jsou tam dva. Musíš napsat obě parciální derivace. Ty jsi napsal jen jednu hybridní (vlastně jsi položil 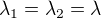 a pak derivoval podle
a pak derivoval podle  ).
).
Offline
#21 26. 08. 2011 09:59
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: viazane extremy u=xyz
↑ vysoka:
Zdravím,
když odečteš (1)-(2), (1)-(3), (2)-(3), tak po úpravě na součinový tvar dostávaš např. 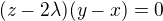 , výsledky odsud už se dají použít pro dosazování do poslední rovnice a následně do předposlední.
, výsledky odsud už se dají použít pro dosazování do poslední rovnice a následně do předposlední.
Snad to postačí.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » viazane extremy u=xyz (TOTO TÉMA JE VYŘEŠENÉ)
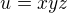 ak
ak 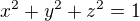 a zaroven
a zaroven 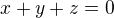
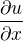
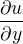
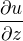 a uprava vazieb na
a uprava vazieb na