Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 06. 2011 11:24
Goniometrická rovnice
Dobrý den,
řeším následující příklad:
Kolik x náleží do intervalu  ? Správná odpověď: 1
? Správná odpověď: 1
Počítám takto:
 -tedy mám 1 kořen v intervalu.
-tedy mám 1 kořen v intervalu. - zde mi po úpravě na absolutní hodnotu vycházejí 4 kořeny, které bych zahrnul do výsledku, tam má být ale pouze 1 kořen.
- zde mi po úpravě na absolutní hodnotu vycházejí 4 kořeny, které bych zahrnul do výsledku, tam má být ale pouze 1 kořen.
Děkuji za pomoc.
Offline
- (téma jako vyřešené označil(a) joinusman)
#2 21. 06. 2011 11:50
Re: Goniometrická rovnice
↑ joinusman:
tu úpravu máš správně, jen máš potom zmatek:
1)
2)
nemá v 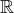 řešení (druhá mocnina je vždy nezáporná)
řešení (druhá mocnina je vždy nezáporná)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline

 :
:
