Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 06. 2011 14:55
Rovnosť polynómov
Zdravím..Prepáčte, že toľko otravujem...Potreboval by som podrobne ako vzorový vysvetliť jeden príklad. Ak sa niekto nájde, tak fakt ďakujem :)
Nájdi všetky mnohočleny F(x), pre ktoré platí rovnosť: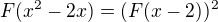
Ďakujem :):):)
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 17. 06. 2011 15:19 Příspěvek uživatele OiBobik byl skryt uživatelem OiBobik. Důvod: blbost
#3 17. 06. 2011 15:35
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Rovnosť polynómov
Odkud je x?
"Máte úhel beta." "No to nemám."
Offline
#4 17. 06. 2011 15:42 — Editoval musixx (17. 06. 2011 15:48)
Re: Rovnosť polynómov
↑ check_drummer: Hraje to nějakou roli? Tak ať je transcendentní nad patřičným okruhem/tělesem, jak už to u polynomů bývá...
Offline
#5 17. 06. 2011 16:02 — Editoval check_drummer (17. 06. 2011 16:14)
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Rovnosť polynómov
↑ musixx:
Opravuji: Je však nutno vědět, jaké hodnoty může může polynom mít, tj. nad jakým okruhem/tělesem jej uvažujeme.
"Máte úhel beta." "No to nemám."
Offline
#6 17. 06. 2011 16:07 — Editoval check_drummer (18. 06. 2011 11:11)
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Rovnosť polynómov
Myšlenky:
Argumenty F se rovnají pro x=2 nebo x=1. Pro ta vychází F(0)=0 nebo 1, F(-1)=0 nebo 1.
Zřejmě konstantní funkce =0 nebo =1 vyhovuje. Předpokládejme dále nekonstantní polynom.
1)Pro x=0 máme buď a) F(0)=0=F(-2) nebo b) F(0)=1 a F(-2)=+-1.
2)Koeficient u nejvyšší mocniny x musí být 1 (dle rovnosti polynomů).
3)Rovněž mi vychází koeficient u druhé nejvyšší mocniny roven n (je-li nejvyšší mocnina x^n).
4)Zkoumejme, zda nějaký lineární polynom nemůže splňovat uvedenou podmínku - je jediný a sice tvaru "x+1" (koeficient u x musí být 1 dle 2) a absolutní člen se pak snadno odvodí).
5)Pokud G,H splňují uvedený vztah, pak jej splňuje i jejich součin G.H, tedy řešením jsou všechny polynomy tvaru  pro i >= 1 přirozené.
pro i >= 1 přirozené.
6) Platí-li 1a), pak F má absolutní člen = 0.
7) Platí-li 1b) Pak má f absolutní člen = 1.
...to be continued
"Máte úhel beta." "No to nemám."
Offline
#7 17. 06. 2011 16:37
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Rovnosť polynómov
↑ musixx:
Při dalších úvahách musím polemizovat - např. vím-li, že x je z množiny reáných čísel, pak mohu použít limitní úvahy. Kdežto nevím-li to, nemohu... Nebo lze nějak formálně použít limitní přechod, aniž budu "dosazovat" ("neomezeně velké" hodnoty) za x?
"Máte úhel beta." "No to nemám."
Offline
#8 18. 06. 2011 11:00
Offline
#9 18. 06. 2011 11:12
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Rovnosť polynómov
↑ BakyX:
To ještě není úplné řešení - ještě je nutné ukázat, zda neexistují jiná řešení... A to je na tom asi to nezajímavější. :-)
"Máte úhel beta." "No to nemám."
Offline
#10 18. 06. 2011 23:15
Re: Rovnosť polynómov
V oficiálnom riešení stojí:
Mám najprv vyriešiť rovnosť F(x^2) = F^2(x) a potom pomocou nej a substitúcie y=x-1 dostanem riešenie (x+1)^n. Alebo tak nejak
Akosi sa mi nedarí tú substitúciu napasovať. Riešenie pre F(x^2) = F^2(x) je x^n
1^6 - 2^6 + 3^6 = 666
Offline
#11 19. 06. 2011 12:42
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Rovnosť polynómov
Myslím, že úloha by se mohla přesunout do Zajímavých úloh z algebry (totéž i Tvé ostatní úlohy o polymomech ze sekce Střední škola).
"Máte úhel beta." "No to nemám."
Offline
#12 19. 06. 2011 22:26 — Editoval anes (19. 06. 2011 22:34)
Re: Rovnosť polynómov
Téma je sice vyřešené, ale úplné řešení tu ještě nevidím a úloha je to zajímavá, tak pro změnu moje úvahy.
Předpokládám, že pracujeme s polynomy s reálnými koeficienty. Já bych na to šel asi přes zápis polynomu pomocí součinu kořenových činitelů.
Jak už někdo psal, vedoucí koeficient polynomu je od pohledu 1, takže se s ním dál nebudu otravovat. Taky si, než začnu, v zápisu posunu x, aby se mi na to lépe koukalo (čistě otázka vkusu, nemá na úlohu vliv). Budu tedy hledat polynomy, kde  .
.
Až na nějaké ty konstatní případy zapíšu náš polynom stupně n jako 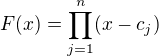 kde
kde  jsou kořeny, ne nutně různé. (násobnost je zbytečné extra zkoumat). To, že polynom můžu takto zapsat je vlastně taky přímý důsledek Bezoutovy věty.
jsou kořeny, ne nutně různé. (násobnost je zbytečné extra zkoumat). To, že polynom můžu takto zapsat je vlastně taky přímý důsledek Bezoutovy věty.
Podobně zapíšu  ,
,  .
.
Tyto dva polynomy G, H se budou rovnat právě když budou mít stejné kořeny (s odpovídající nasobností), budu tedy zkoumat, kdy to nastane.
Kořeny G budou zřejmě naše 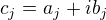 , kořeny H budou
, kořeny H budou  takové, že
takové, že  .
.
Pokud bude  , pak máme hezkou kvadratickou rovnici a
, pak máme hezkou kvadratickou rovnici a 
Pokud to štěstí nemáme, zůstaneme u  .
.
Teď pár postřehů. Z reálného  se vylíhnou dva (resp. jeden dvojnásobný) kořeny H, reálné nebo komplexní. Z komplexního
se vylíhnou dva (resp. jeden dvojnásobný) kořeny H, reálné nebo komplexní. Z komplexního  (tedy
(tedy  ) ale reálný kořen H nikdy nevznikne. Pokud bude m
) ale reálný kořen H nikdy nevznikne. Pokud bude m  reálných, bude mít G 2m reálných kořenů (resp. # * násobnost) a 2m reálných kořenů potřebuji i pro H. Proto nutně
reálných, bude mít G 2m reálných kořenů (resp. # * násobnost) a 2m reálných kořenů potřebuji i pro H. Proto nutně  , abych měl nezáporný diskriminant v té kvadr. rovnici a měl tím pádem dost reálných kořenů H.
, abych měl nezáporný diskriminant v té kvadr. rovnici a měl tím pádem dost reálných kořenů H.
Kdyby ale zase  , pak by mi v H vylezl kořen < -1 a musel by být i kořenem G, potažmo F, což nelze. Z reálných
, pak by mi v H vylezl kořen < -1 a musel by být i kořenem G, potažmo F, což nelze. Z reálných  tedy zbývá jen -1, která zřejmě už funguje.
tedy zbývá jen -1, která zřejmě už funguje.
Jediný reálný kořen, který může F mít je tedy -1.
Co se týče komplexních kořenů, tam mě nenapadá nic chytřejšího, než zkoumat řešení té rovnice  .
.
Z rovnosti imaginárních částí 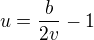 a po dosazení do reálné části a pár úpravách
a po dosazení do reálné části a pár úpravách 
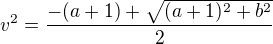 (chceme v reálné, takže minus odmocnina by neměla smysl).
(chceme v reálné, takže minus odmocnina by neměla smysl).
Pro každou dvojici a,b tak dostáváme dvě různá řešení:  a
a  .Každému z celkových m komplexních kořenů F jsem tedy jednoznačně přiřadil dva kořeny H. Protože ale má platit H=G a G má všechny kořeny aspoňdvojnásobné po dvou stejné, potřeboval bych spárovat i kořeny H. Potřeboval bych tedy vždy najít aspoň dvě různá
.Každému z celkových m komplexních kořenů F jsem tedy jednoznačně přiřadil dva kořeny H. Protože ale má platit H=G a G má všechny kořeny aspoňdvojnásobné po dvou stejné, potřeboval bych spárovat i kořeny H. Potřeboval bych tedy vždy najít aspoň dvě různá  , která dají při stejném
, která dají při stejném  stejné řešení
stejné řešení  . To se ale za žádných podmínek nepodaří, protože derivováním zjistíme, že
. To se ale za žádných podmínek nepodaří, protože derivováním zjistíme, že 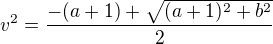 jako funkce a je na R prostá.
jako funkce a je na R prostá.
Takže konstantní polynomy 0, 1 a 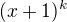 jsou podle mě opravdu jediné splňující podmínku
jsou podle mě opravdu jediné splňující podmínku
\\docela rád bych ale viděl nějaké elegantnější řešení, hlavně k těm komplexním kořenům.
Offline
#13 20. 06. 2011 16:11
Re: Rovnosť polynómov
Zdravím..Preštudoval som si podrobne počas najnudnejšieho obdobia dňa (škola) postup, ako riešiť podobný príklad k tomuto a pokúsim sa to tu nejako spísať riešenie tohto príkladu po časť, kde som sa zasekol.
Predpokladajme, že aspoň jeden z koeficientov 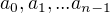 je rôzny od nuly a označme si najvyšší nenulový koeficient indexnom
je rôzny od nuly a označme si najvyšší nenulový koeficient indexnom  . Zrejme
. Zrejme  . Ďalej predpokladajme, že
. Ďalej predpokladajme, že 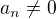 . Danú rovnosť si následne môžeme prepísať takto:
. Danú rovnosť si následne môžeme prepísať takto:
Teraz sa snažíme porovnať koeficienty pri mocninách väčších ako  a menších ako
a menších ako  , lebo také mocniny sa nenachádzajú na ľavej strane. Porovnajme napríklad koeficienty pri mocnine
, lebo také mocniny sa nenachádzajú na ľavej strane. Porovnajme napríklad koeficienty pri mocnine  , pretože je to druhá najväčšia mocnina na pravej strane (hneď po
, pretože je to druhá najväčšia mocnina na pravej strane (hneď po 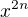 ) a teda sa lepšie vyjadrujú koeficienty pri nej.
) a teda sa lepšie vyjadrujú koeficienty pri nej.
Je vidieť, že mocnina  na pravej strane vznikne iba pri súčte súčinov prvých dvoch členov a podľa binomickej vety je zrejmé, že koeficient pri mocnine
na pravej strane vznikne iba pri súčte súčinov prvých dvoch členov a podľa binomickej vety je zrejmé, že koeficient pri mocnine  bude rovný
bude rovný  . Keďže na ľavej strane je koeficient
. Keďže na ľavej strane je koeficient  , tak dostávame spor z predpokladam, že o existencii reálneho čísla
, tak dostávame spor z predpokladam, že o existencii reálneho čísla  vyhovujúceho podmienkám. Rovnica nám tak prejde do jednoduchšieho tvaru, ktorý môžeme upravovať.
vyhovujúceho podmienkám. Rovnica nám tak prejde do jednoduchšieho tvaru, ktorý môžeme upravovať.
No a teraz sa mi nedarí zistiť dve veci. Či je predchádzajúci postuo skutočne správny a ako pokračovať ďalej :) Ďakujem.
1^6 - 2^6 + 3^6 = 666
Offline
#14 20. 06. 2011 16:42 — Editoval anes (20. 06. 2011 16:48)
Re: Rovnosť polynómov
BakyX napsal(a):
Je vidieť, že mocnina
na pravej strane vznikne iba pri súčte súčinov prvých dvoch členov a podľa binomickej vety je zrejmé, že koeficient pri mocnine
bude rovný
.
Jestli jsem tě správně pochopil, tak problém bude tady.  ti nevyplivne jen x^n, ale všechny mocniny x mezi 1 a n a (hlavně mezi k a n). A
ti nevyplivne jen x^n, ale všechny mocniny x mezi 1 a n a (hlavně mezi k a n). A 
Jinak ano, porovnávání koeficientů je taky způsob, ikdyž u téhle úlohy jsem v tom neviděl nic pěkného. Dostal jsem se asi tak daleko jako ↑ check_drummer:, pak už jsem se v sumách s kombinačními čísly patlat nechtěl. Ale možná tam je nějaká finta, na kterou jsem nepřišel.
EDIT: na levé straně taky nevidím důvod, proč by měl být koeficient u  nula.
nula.
Offline
#15 20. 06. 2011 17:08 — Editoval BakyX (22. 06. 2011 17:27)
Re: Rovnosť polynómov
↑ anes:
Tak ja potom fakt neviem ! Tá kniha je písaná takým štýlom, že neviem riešiť úlohy a ani nechápem oficiálnemu riešeniu. Asi som jednoduchu blbý.
Oficiálne riešenie od slova do slova !
Označte y=x-1 a G(y)=F(y-1) a porovnajte s 3.7, řešením sú kromě nulového mnohočlenu mnohočleny F(x)=(x+1)^n, kde  .
. 
1^6 - 2^6 + 3^6 = 666
Offline
#17 22. 06. 2011 21:15
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Rovnosť polynómov
↑ anes:
Ahoj, mám dotazy:
- proč c<-1 nemůže být kořen F?
- proč při párování kořenů předpokládáš, že ke dvěma různým a musí být stejné b? Nemohou různá a1,b1 a a2,b2 nakonec "vygenerovat" nějaký "společný" kořen?
Díky
"Máte úhel beta." "No to nemám."
Offline
#18 22. 06. 2011 21:33
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Rovnosť polynómov
↑ BakyX:
Tou substitucí vlastně dostaneš - pro G(x)=F(x-1)  , tj.
, tj.  , tj.
, tj.  , tj. G(x)=x^n a tedy F(x)=(x+1)^n.
, tj. G(x)=x^n a tedy F(x)=(x+1)^n.
"Máte úhel beta." "No to nemám."
Offline
#19 22. 06. 2011 21:56 — Editoval BakyX (22. 06. 2011 22:15) Příspěvek uživatele BakyX byl skryt uživatelem BakyX.
#20 23. 06. 2011 00:54 Příspěvek uživatele BakyX byl skryt uživatelem BakyX.
#22 23. 06. 2011 12:18 — Editoval musixx (23. 06. 2011 12:25)
Re: Rovnosť polynómov
Máme něco ukázat o polynomu F (konkrétně 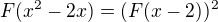 ).
).
Toto tvrzení převedeme na tvrzení o polynomu G, který splňuje pro všechna z, že G(z)=F(z-1). {schválně používám jiné písmenko, aby to nemátlo}
Tedy rovnost  se odnikud nevzala a nikdo na začátku netvrdí, že platí, ta se má dokázat.
se odnikud nevzala a nikdo na začátku netvrdí, že platí, ta se má dokázat.
Jak převedeme tvrzení o polynomu F na tvrzení o polynomu G? No protože G(z)=F(z-1), tak také F(u)=G(u+1).
Proto je  (roli
(roli  tady hraje
tady hraje 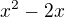 ) a podobně na pravé straně vznikne
) a podobně na pravé straně vznikne  .
.
Tvrzení o F je tak převedeno na tvrzení o G, a to  . Klidně pišme
. Klidně pišme  a máme proto dokázat, pro jaké polynomy G platí
a máme proto dokázat, pro jaké polynomy G platí  . To je snadné a převod zpět "do F" je v mém značení jen dosazování do jednoduchých substitucí pro y a u.
. To je snadné a převod zpět "do F" je v mém značení jen dosazování do jednoduchých substitucí pro y a u.
Asi jsem to psal zbytečně podrobně, ale je postup z knížky už teď jasný?
EDIT: Přes PM jsem se od jeleny dověděl, že jsi ještě na základce, což mě hodně udivilo. Proto jsem napsal podrobnější vysvětlení než se možná v sekci Zajímavých úloh z algebry bežně dělá.
Offline
#23 23. 06. 2011 12:31
Re: Rovnosť polynómov
↑ musixx:
Ďakujem za fakt pekný prístup :) Škoda, že tie vysvetlenia v tej knihe nie sú takéto - ušetrilo by mi to veľa času. Knihu, kde je algebra vysvetlená lepšie, bohužial nemám.
Používa sa tento trik s definovaním nového polynómu často ? Je celkom zaujímavý..
Ešte raz ďakujem.
1^6 - 2^6 + 3^6 = 666
Offline
#24 23. 06. 2011 12:45 — Editoval musixx (23. 06. 2011 12:49)
Re: Rovnosť polynómov
To už je bohužel tak trochu úděl pokročilejších knih -- jen naťuknout a předpokládá se dostatečně zdatný čtenář.
Jen pro ilustraci, jeden příklad z mnoha: Když jsme na semináři z teorie čísel studovali knihu Irelanda a Rosena A Classical Introduction to Modern Number Theory a dostali se tam už kousek dál, tak si pořád pamatuji jeden důkaz. Začínal oblíbeným "It is easy to see." No, touto větou jsme strávili více než dva semináře a bez odborného vedení přednášejícího si myslím, že nikdo z posluchačů by neměl šanci "tu jednoduchost vidět".
Offline
#25 23. 06. 2011 12:55
Re: Rovnosť polynómov
↑ musixx:
Možno je to naschvál tak, aby sa na tým čitateľ natrápil a lepšie si učivo zapamätal neviem. V každom prípade, nepoznáš nejakú inú knihu k štúdiu takýchto základov algebry ?
1^6 - 2^6 + 3^6 = 666
Offline

 ? Ty snad všude. Byla-li by k mání konečná charakteristika, tak snad i další polynomy by se daly najít -- jen tipuju, nemám na to teď čas řešit.
? Ty snad všude. Byla-li by k mání konečná charakteristika, tak snad i další polynomy by se daly najít -- jen tipuju, nemám na to teď čas řešit.