Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Analytická geometrie (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 06. 2011 19:28
Analytická geometrie
Ahoj, mám problém s touto úlohou -
Na přímce p: x+y-4 = 0 najděte takový bod, ze kterého je vidét úsečka AB pod úhlem 45 stupňů. Body A = (3,3), B = (0,2)
Možné řešení - Body, jelikož leží na přímce, budou mít souřadnice X = (4-y, y). Co byste poradili dále?
Offline
- (téma jako vyřešené označil(a) Miki314)
#2 26. 06. 2011 19:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analytická geometrie
Zdravím,
bod na přímce je P, potom bych uvažovala použití vzorce pro odchylku vektorů nebo odchylku přímek PA a PB (a řešení rovnice s jednou neznámou y). Může být? Děkuji.
Offline
#3 26. 06. 2011 20:06
Re: Analytická geometrie
↑ jelena:
Metoda navžená ↑ jelenou: 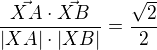
vede k rovnici 4 stupně, ale dá se to pěkně rozložit.
Dostaneš 4 řešení
ale dvě z nich odpovídají úhlu 135°, takže je musíš odhalit a vyloučit.
OT: pro Jelenu - uvádím to proto, že když už jsem se s tím počítal, tak nechci, aby to přišlo nazmar.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 26. 06. 2011 20:08 Příspěvek uživatele Miki314 byl skryt uživatelem Miki314. Důvod: nalezeno řešení jiným uživatelem
#5 26. 06. 2011 20:23
#6 26. 06. 2011 20:33
Re: Analytická geometrie
↑ Miki314:
První dva řádky jsou dobře, třetí (poslední) už nějsem schopen rozluštit, ale umocníš a mělo by ti vyjít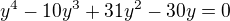
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 26. 06. 2011 20:39
Re: Analytická geometrie
↑ zdenek1:
No, a co s tím dále? Nejak se pořád nemůžu dopracovat k vysledku..
Offline
#8 26. 06. 2011 20:42
Re: Analytická geometrie
↑ Miki314:
Dopracoval ses k této rovnici?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#10 26. 06. 2011 20:54
Re: Analytická geometrie
↑ Miki314:
Tak nyní přichází nejzajímavěší část![kopírovat do textarea $y[(y^3-5y^2)-(5y^2-25y)+(6y-30)]=0$](/mathtex/df/df133b0c88e907b2f41e388c501f2860.gif)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#12 26. 06. 2011 21:03
Re: Analytická geometrie
↑ Miki314:
Rozložit na součin lineárních členů.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#13 26. 06. 2011 21:14
#14 26. 06. 2011 21:27
Re: Analytická geometrie
↑ Miki314:
ANo, ze všech kulatých závorek vytkni 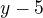 - ale toto nepatří do sekce VŠ
- ale toto nepatří do sekce VŠ
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#15 26. 06. 2011 21:33
Re: Analytická geometrie
↑ zdenek1:
Horko těžko, ale nakonec se mi to snad povedlo.. Uff.. Děkuju za Tvoje (Vaše) rady a za čas.. Vyřešeno...
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Analytická geometrie (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $[-1;5]$](/mathtex/95/955148c334f77108c007b2f6f998a00e.gif) ,
, ![kopírovat do textarea $[1;3]$](/mathtex/7e/7eb1e096e40d37162b1d7f1d6202477d.gif) ,
, ![kopírovat do textarea $[2;2]$](/mathtex/b9/b94b8a29c9399843554c050b232cc7db.gif) a
a ![kopírovat do textarea $[4;0]$](/mathtex/38/381671226e4f9bd90d94dda7e21909dc.gif)
