Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 07. 2011 12:58
1 a 2 derivace
Ahoj
Potřeboval bych poradit a první a druhou derivací
funkce je (x^2+1)/x
první derivace mi vyšla (x^2-1)/x^2 - to si myslím že mi vyšlo dobře
ale druhá derivace mi jednou vyšla :)) (3x^2-1)/x^3 ,
pak mi taky vyšla (2x)/X4 z čehoš by X při počítání kovexnosti a konkávnosti vyšlo X=0
nebo se to dalo ještě upravit - z čehoš by ale vzniklo (2)/X^3 z čeho by ale x nevyšlo
Můžete mi někdo poradit - popř jestli vám vyšlo něco jiného ukázat kde se mi vloudila chybka - díky
Offline
- (téma jako vyřešené označil(a) rdrimmer)
#2 03. 07. 2011 13:33 — Editoval Hanis (03. 07. 2011 13:36)
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: 1 a 2 derivace
Vždycky se snaž maximálně upravit před derivací do výhodných tvarů - součtů apod...
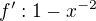

Vzhledem k tomu, že původní fce není definována pro x=0, je logické, že ani její derivace v tomto bodě není definována.
Offline
#3 03. 07. 2011 13:33
Re: 1 a 2 derivace
↑ rdrimmer:
asi by bolo lepšie si prepísať prvú deriváciu na tvar: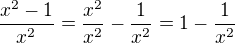
teraz sa bude druhá derivácia určovať lepšie.
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#4 03. 07. 2011 13:36
Re: 1 a 2 derivace
↑ rdrimmer:
zdravím, ta první je dobře a ta druhá je tvuj druhý případ, tedy .
Offline
#5 03. 07. 2011 13:39
Re: 1 a 2 derivace
↑ hradecek:
aha a co je z toho výsledku U a co V? jsem z toho trošku zmaten
Offline
#7 03. 07. 2011 13:43 — Editoval hradecek (03. 07. 2011 13:46)
Re: 1 a 2 derivace
↑ rdrimmer:
U a V ? myslíš funkcie...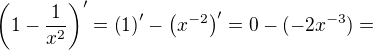

Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#8 03. 07. 2011 13:44 — Editoval Hanis (03. 07. 2011 13:49)
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: 1 a 2 derivace
↑ rdrimmer:
rovnice 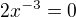 nemá řešení
nemá řešení
Offline
#9 03. 07. 2011 13:47
Re: 1 a 2 derivace
↑ hradecek:
Aha - to hledím - mě u toho derivování dělá problém kdy že je to na -2 - to mi nedošlo .že se to vlastně odečte a bude z toho na -3 .díky
Offline
#10 03. 07. 2011 13:50
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: 1 a 2 derivace
↑ rdrimmer:
jestli chceš určit průběh fce, tak doporučuji určit maxima a minima, asymptotu a z toho už konvexnost/konkávnost vyčteš snadno :-)
Offline