Skrytý text:Hľadáme

v tvare
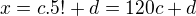
, kde
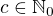
,

. Dosadíme do zadania:
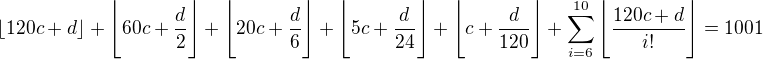
Použijem formulku
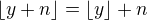
,

(ľahko ide odvodiť z definície floor function).
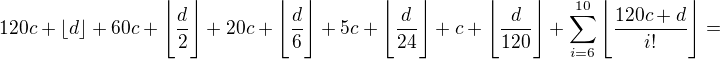

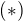
Odhadneme

tak, aby
![kopírovat do textarea $206c\le 1001 \rightarrow c\in [0,4]$](/mathtex/a0/a0c8be0b7bd85828d80b570cdf0b77a8.gif)
.
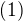

Teraz je potrebné nájsť nejaké

, a potom na základe vlastnosti floor function nájdeme zvyšné reálne

.

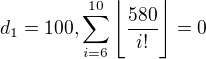
, pretože
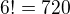
a pre

(v našom prípade je dokonca

), kde

je
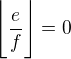
, teda stačí uvažovať

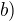
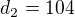
,

.
Jedným riešením je teda
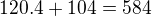
. Podľa definície floor function platí:

.Aplikujeme tuto definíciu na jednotlivé členy
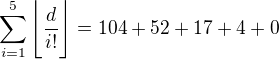
(práve v tomto poradí).
Z prvého členu
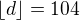
vidíme, že
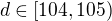
. Teraz je potrebné dokázať, že aj funkčná hodnota ostatných členov sa nezmení pre ľubovolné

z uvedeného intervalu. Funkcia
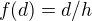
,
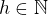
je rastúca, stačí uvažovať hraničné body intervalu t.j 104,105 (pre 104 sme to ukázali, a pre 105 je to jednoduché a platí to), pretože

,

tak, potom
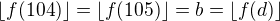
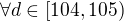
. Teda riešením je

.
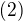
![kopírovat do textarea $c\in [0,3]$](/mathtex/c2/c293e83f36af079eced261cb5ad89788.gif)
ukážeme, že neexistuje také

,

, aby
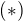
platila. Platí:

, teda potrebujeme

(
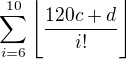
neuvažujeme z rovnakého dôvodu ako v

), ale pre

platí:

, vezmeme najväčšie

(ktoré nemôžeme ani dosiahnuť) -
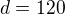
a ukážeme, že

, teda

.
Zadanie platí pre
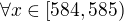
.
Edit=red

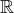 řeště rovnici
řeště rovnici 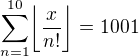 .
.
 v tvare
v tvare 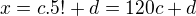 , kde
, kde 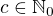 ,
,  . Dosadíme do zadania:
. Dosadíme do zadania: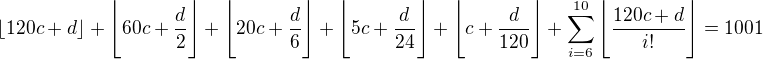
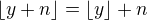 ,
,  (ľahko ide odvodiť z definície floor function).
(ľahko ide odvodiť z definície floor function).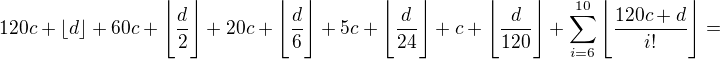

 tak, aby
tak, aby ![kopírovat do textarea $206c\le 1001 \rightarrow c\in [0,4]$](/mathtex/a0/a0c8be0b7bd85828d80b570cdf0b77a8.gif) .
.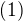

 , a potom na základe vlastnosti floor function nájdeme zvyšné reálne
, a potom na základe vlastnosti floor function nájdeme zvyšné reálne  .
.
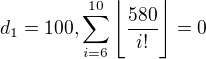 , pretože
, pretože 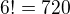 a pre
a pre  (v našom prípade je dokonca
(v našom prípade je dokonca  ), kde
), kde  je
je 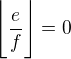 , teda stačí uvažovať
, teda stačí uvažovať 
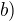
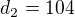 ,
,  .
.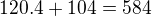 . Podľa definície floor function platí:
. Podľa definície floor function platí:  .Aplikujeme tuto definíciu na jednotlivé členy
.Aplikujeme tuto definíciu na jednotlivé členy 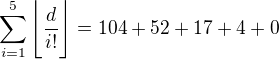 (práve v tomto poradí).
(práve v tomto poradí).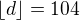 vidíme, že
vidíme, že 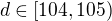 . Teraz je potrebné dokázať, že aj funkčná hodnota ostatných členov sa nezmení pre ľubovolné
. Teraz je potrebné dokázať, že aj funkčná hodnota ostatných členov sa nezmení pre ľubovolné 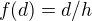 ,
, 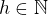 je rastúca, stačí uvažovať hraničné body intervalu t.j 104,105 (pre 104 sme to ukázali, a pre 105 je to jednoduché a platí to), pretože
je rastúca, stačí uvažovať hraničné body intervalu t.j 104,105 (pre 104 sme to ukázali, a pre 105 je to jednoduché a platí to), pretože  ,
,  tak, potom
tak, potom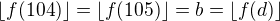
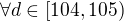 . Teda riešením je
. Teda riešením je  .
.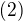
![kopírovat do textarea $c\in [0,3]$](/mathtex/c2/c293e83f36af079eced261cb5ad89788.gif) ukážeme, že neexistuje také
ukážeme, že neexistuje také  , aby
, aby  , teda potrebujeme
, teda potrebujeme  (
(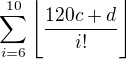 neuvažujeme z rovnakého dôvodu ako v
neuvažujeme z rovnakého dôvodu ako v  ), ale pre
), ale pre  , vezmeme najväčšie
, vezmeme najväčšie 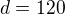 a ukážeme, že
a ukážeme, že  , teda
, teda  .
. 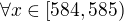 .
.