Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 07. 2011 13:25
- Alenka.Janská
- Příspěvky: 181
- Reputace: 3
podivnej výsledek rovnice
ahoj, jedna rovnice mi vyšla skutečně hezky, ale řešení má být průnik množin (-1,1)
ne to co mi vyšlo...
už fakt nevím co s tím
Jo, opravdu si vážím veškeré projevené pomoci... :)
Offline
- (téma jako vyřešené označil(a) Alenka.Janská)
#2 13. 07. 2011 13:28 — Editoval ((:-)) (13. 07. 2011 14:35)
Re: podivnej výsledek rovnice
↑ Alenka.Janská:
Riešením tejto rovnice je každé reálne číslo okrem -1 a 1. Riešil Ti ju už Cheop v niektorom predchádzajúcom príspevku.
Odkaz
Prečo dávaš dvakrát tú istú rovnicu?
Tvoja chyba: v druhom riadku pred číslom 2 má byť +.
Platí totiž, že 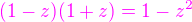 a menovateľ druhého zlomku je
a menovateľ druhého zlomku je 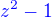 ,
,
to sú presne opačné znamienka, takže treba vyňať -1 a tá zmení znamienko pred zlomkom na + 
Ďalej:
Offline
#3 13. 07. 2011 13:33
Re: podivnej výsledek rovnice
↑ Alenka.Janská: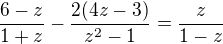 podmínky:
podmínky: 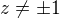
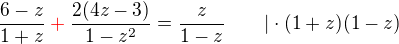
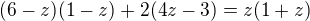
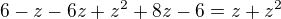
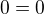
Řešení: 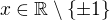
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 13. 07. 2011 14:21 — Editoval Rumburak (13. 07. 2011 16:55)
Re: podivnej výsledek rovnice
↑ Alenka.Janská:
Už po několikáté v podstatě stále tatáž chyba. Rozeberme to hodně podrobně:
Na levé straně je druhým zlomkem  (beru ho včetně předcházejícího znaménka "minus"),
(beru ho včetně předcházejícího znaménka "minus"),
jehož jmenovatele 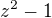 můžeme rozložit na součin
můžeme rozložit na součin 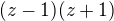 , takže
, takže
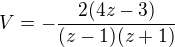
Po vynásobění výrazem 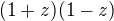 dostaneme
dostaneme
(1)  .
.
Ve zlomku na pravé straně v (1) můžeme bezprostředně vykrátit činitel 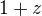 v čitateli s činitelem
v čitateli s činitelem  ve jmenovateli,
ve jmenovateli,
protože podle komutativního zákona pro sčítání je 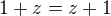 . Tímto opravdu triviálním vykrácením obdržíme
. Tímto opravdu triviálním vykrácením obdržíme
(2)  .
.
Pokud máme něčím krátit zlomek na pravé straně v (2), pak už to nebude tak jednoduché jako prve, protože žádný činitel v čitateli není
bezprostředně přítomen ve jmenovateli. Takovou situaci zde ale přesto můžeme navodit, a sice pomocnou úpravou prostřednictvím
rovnosti 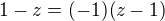 :
:
(3)  .
.
Nyní už krátit můžeme, a sice výrazem 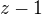 :
:
 .
.
(Všimni si, že znaménko "minus" zmizelo.)
POZNÁMKA: Komutativní zákon platí pro sčítání a násobení, avšak NEPLATÍ pro odčítání ani pro dělení.
Offline

