Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 08. 2011 13:49
Elastické deformace těles - příklady
Zdar, potřebuji pomoct s několika příklady, k výsledkům jsem dobral, ale především příkladu s vnitřním tlakem v trubce dobral, si nejsem jistý správností.
1) Hliníkový drát průměru 1mm a délky 2m je vodorovně natažen a na koncích upevněn. Ke středu drátu bylo zavěšeno závaží 0,25kg. O kolik poklesl střed drátu? Youngův modul pružnosti v tahu hliníku je 71 GPa.
2) Závaží o hmotnosti 200g se na závěsu otáčí v horizontální rovině s frekvencí 120 ot/min. Určete elastické prodloužení závěsu, je-li známo, že tahová síla 10N prodlouží závěs o 1cm. Počáteční délka závěsu je 50cm, hmotnost závěsu a účinek tíhy zanedbat.
3) Drát původní délky 10m je na jednom konci upevněn a na druhém napínán silou velikosti 200N, čímž se prodlouží o 4 mm. Určit původní průměr drátu a jeho změnu při prodloužení, když materiál, ze kterého je drát zhotoven, má modul pružnosti v tahu 200GPa a ve smyku 75GPa.
4) Ocelový sloup tvaru hranolu a délky 5m, s příčnými hranami délky 10cm, je namáhán tahovým napětím 0,1MPa ve směru délky. Jak se změní objem tohoto sloupu protažením? Modul pružnosti oceli v tahu je 200GPa a ve smyku 79GPa.
5)Jak velký vnitřní tlak vydrží skleněná trubka, jejíž vnější poloměr je 4mm a vnitřní 3,5mm? Mez pevnosti skla je 30MPa.
6) Jakou délku by musel mít ocelový drát kruhového průřezu zavěšený na jednom konci, aby se roztrhl vlastní vahou? Hustota oceli je 7800kg/m3, mez pevnosti oceli je 800MPa.
Mé výsledky: 1) h=0,94cm (průhyb jsem bral jako lineární (tzn. pythágorova věta), jinak nevím)
2)/delta l=1,6cm
3)předpokládám, že je to v podstatě stejný problém jako 4), tzn. /epsilon příčná=(d-d0)/d0
4)/delta V=11,7mm2
5)p=0,7MPa (pravděpodobně špatně)
6)l=10 455m
Budu rád, pokud si někdo najde chvilku a přepočítá to a nebo alespoň poradí s tou skleněnou trubkou. Díky.
Offline
- (téma jako vyřešené označil(a) Tscar)
#2 10. 08. 2011 22:18
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Elastické deformace těles - příklady
↑ Tscar:
Zkusím něco napsat k té skleněné trubce, i když letmým pohledem budou problémy i jinde (např. hned v první úloze). V každém zadání by mělo být uvedeno, jaká zjednodušení můžeme použít (tím nekritizuju tvůj dotaz, předpokládám, že zadání je přepsáno úplně). Nejjednodušším výpočetním modelem je tzv. membrána. Tento model předpokládá v materiálu rovinnou napjatost a pracuje jen se střední tloušťkou stěny. Jindy se používá model tlustostěnné nádoby, kde už myslím uvažujeme trojosou napjatost, ale o tom moc nevím. I v ostatních uvedených úlohách se řešení podstatně liší podle toho, kolik toho zanedbáme (např. vlastní tíhu). Teď konkrétně:
Pro rotačně symetrické membrány jde odvodit Laplaceovu rovnici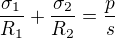 , kde
, kde 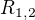 jsou hlavní poloměry křivosti,
jsou hlavní poloměry křivosti, 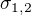 napětí v příslušných směrech,
napětí v příslušných směrech,  tlak v nádobě a
tlak v nádobě a  tloušťka stěny. V případě trubky je zřejmě jedna z hlavních křivostí nulová (a tedy poloměr křivosti nekonečný), zvolme
tloušťka stěny. V případě trubky je zřejmě jedna z hlavních křivostí nulová (a tedy poloměr křivosti nekonečný), zvolme 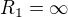 , za druhý vezmu aritmetický průměr vnitřního a vnějšího poloměru:
, za druhý vezmu aritmetický průměr vnitřního a vnějšího poloměru: 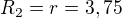 mm. Odtud plyne dosazením do Laplaceovy rovnice jedno hlavní napětí, nazývané tečné:
mm. Odtud plyne dosazením do Laplaceovy rovnice jedno hlavní napětí, nazývané tečné: 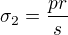 . Druhé hlavní napětí (osové) můžeme odhadnout podle obrázku:
. Druhé hlavní napětí (osové) můžeme odhadnout podle obrázku: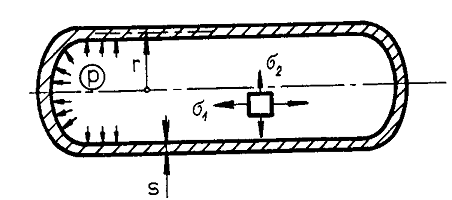
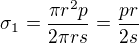 .
.
Na základě předpokladu rovinné napjatosi je  . Další postup se mírně liší podle toho, kterou hypotézu pevnosti použijeme. O skle toho moc nevím, ale kdyby šlo použít stejné teorie jako pro ocel, tak dostaneme např. podle teorie
. Další postup se mírně liší podle toho, kterou hypotézu pevnosti použijeme. O skle toho moc nevím, ale kdyby šlo použít stejné teorie jako pro ocel, tak dostaneme např. podle teorie 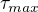 :
: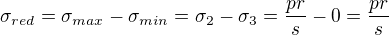 . (Víme, že obě napětí budou tahová, tedy kladná, proto
. (Víme, že obě napětí budou tahová, tedy kladná, proto  ).
).
Teď stačí porovnat toto redukované napětí s mezí pevnosti.  . Podle jiné hypotézy pevnosti by výsledek vyšel o něco jinak. Taky je třeba si uvědomit, že při tomhle tlaku už trubička praskne, takže s ohledem na to a taky na veliká zjednodušení při výpočtu to chce nešetřit na součiniteli bezpečnosti. Reálná trubka je vždycky namáhána i ohybem atd., prostě chci říct, že tohle je takový první odhad před opravdovým výpočtem. :) Samozřejmě tam může někde být chyba...
. Podle jiné hypotézy pevnosti by výsledek vyšel o něco jinak. Taky je třeba si uvědomit, že při tomhle tlaku už trubička praskne, takže s ohledem na to a taky na veliká zjednodušení při výpočtu to chce nešetřit na součiniteli bezpečnosti. Reálná trubka je vždycky namáhána i ohybem atd., prostě chci říct, že tohle je takový první odhad před opravdovým výpočtem. :) Samozřejmě tam může někde být chyba...
Offline
#3 10. 08. 2011 22:41
Re: Elastické deformace těles - příklady
↑ FliegenderZirkus:
Zadání je opsáno úplně. Nebojím se říct, že zjednodušení lze vzít maximální možné. K dispozici nejsou tabulky a nepředpokládá se znalost velikosti žádného koeficientu. Abych přiblížil situaci, jsou to příklady pro absolvování Fyziky 1 mechaniky na VŠ technického směru. Hodinová dotace byla 1 přednáška a 1 cvičení týdně po jeden semestr. Asi tak pro představu.
Díky za ten výpočet, vypadá to velmi zajímavě. Opravdu jen hodně rychle jsem si prohlédl skripta předmětu Pružnost a pevnost a myslím, že tohle mě bude čekat tam. Ale pochopil jsem, takže se to nebudu bát zneužít.
Pokud by to někdo ale ještě trochu zjednodušil, byl bych rád.
Offline
#4 10. 08. 2011 23:09
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Elastické deformace těles - příklady
↑ Tscar:
Já myslel, že to zadání je právě z pružnosti a pevnosti. Možná se teda chce jen obrázek - pohled ve směru osy a příslušná rovnováha sil, tj. úplně to redukovat na jednoosou napjatost. Zajímavé je, že v případě té hypotézy 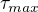 vyjde dovolený tlak stejně (u jiných hypotéz už ne).
vyjde dovolený tlak stejně (u jiných hypotéz už ne).
Přepočítal jsem
2) 1,58 cm,
4) stejně, jen tam je překlep v jednotkách :)
6) stejně
Nad tou jedničkou se zkusím zamyslet, třeba dřív poradí někdo z kolegů.
Offline
#5 10. 08. 2011 23:25
Re: Elastické deformace těles - příklady
↑ FliegenderZirkus:
4) překlep v jednotkách? nějak to nevidim .. kolik ti to teda vyšlo?
jak myslíš tu trubku? asi to budu potřebovat trošku víc polopaticky ...
nastínim, jak jsem uvažoval u 2): spočítal jsem omega, z toho dostředivé zrychlení (omega na druhou * r), následně sílu .. a pak jsem vycházel z Hookova zákona, při tom, že E*S je pro oba případy stejné... při výpočtu té síly jsem použil poloměr již prodloužený tou silou o delta l, tam si nejsem uplně jistej ...
Offline
#6 10. 08. 2011 23:26
Re: Elastické deformace těles - příklady
↑ FliegenderZirkus:
a ještě k té jedničce .. nehledej tam složitosti, spíš naopak .... mělo by to být náročností srovnatelné s ostatními ...
Offline
#7 11. 08. 2011 09:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Elastické deformace těles - příklady
Zdravím vás,
myslím, že tuto sbírku jsme postupně řešili 2 roky zpět s kolegou Peťou jeho téma) - konkrétně úlohu 1 jsem navrhovala v tématu (úloha 3). Kolega číselné výsledky měl a asi by se ozval, kdyby nevycházelo.
↑ Tscar:
jinak kontrola číselných výsledku je celkem otročina, lepší je umístit svůj postup, to se lépe kontroluje. Více úloh v tématu je proti pravidlům (co bych dělala, kdybych hned zrana nezacitovala :-)
Snad by stalo za to téma trochu protřídit - co ještě potřebuješ překonzultovat, umístí prosím do samostatného tématu + cituji kolegu ↑ FliegenderZirkus:, co už k tomu poradil.
Kolegovi ↑ FliegenderZirkus: patří velký obdiv a a poděkování.
Offline
#8 11. 08. 2011 09:54 — Editoval FliegenderZirkus (11. 08. 2011 09:58)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Elastické deformace těles - příklady
↑ jelena:
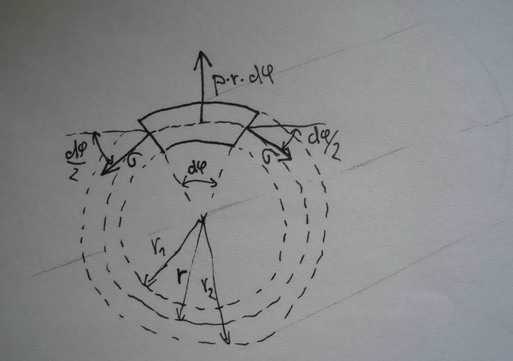
Tento příspěvek není myšlen jako provokace, jen už jsem měl nakreslený obrázek, tak ho pošlu. S více úlohami v tématu máš pravdu, zde už bych v řešení dál nepokračoval.
↑ Tscar:
Těmi jednotkami jsem myslel, že změna objemu by neměla být v 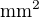 ale
ale 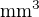 .
.
Obrázek k 5)
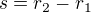
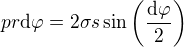
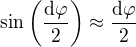
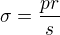
EDIT: Podle tohoto výpočtu tedy v trubičce vznikne stajný typ napjatosti jako při rotaci trubky kolem své osy při uvažování setrvačných účinků (tj. když uvažujeme hustotu - hmotnost). V obou těchto případech se jedná o prostý tah, ve směru osy žádné napjetí není.
Offline
#9 11. 08. 2011 11:59
Re: Elastické deformace těles - příklady
↑ jelena:
Díky, podívám se na to staré téma a případně k 1) a ke 2) založím nové téma
Příště asi dodám i postup. Bude to lepší.
Za více úloh v tématu se omlouvám, měl jsem si přečíst pravidla.
↑ FliegenderZirkus:
Tak ty jednotky jsem parádně přehlíd.
Ta skleněná trubka vypadá skvěle.
Jak psala jelena, samozřejmě ti patří velkej dík.
Offline