Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 06. 2011 14:17
Korene mnohočlenov (jednoduchšia úloha)
Zdravím..Skúste vyriešiť túto peknú úlohu :)
Nech  ,
,  označujú dva rôzne korene mnohočlenu
označujú dva rôzne korene mnohočlenu 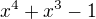 . Dokáž, že ich súčin je koreňom mnohočlenu
. Dokáž, že ich súčin je koreňom mnohočlenu  .
.
Veľa šťastia.
1^6 - 2^6 + 3^6 = 666
Offline
#2 15. 07. 2011 21:25
Re: Korene mnohočlenov (jednoduchšia úloha)
Dobrý den.
Pomocí Wolfu můžeme najít kořeny obou polynomů. Označíme-li kořeny polynomu 4.stupně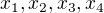 a kořeny polynomu 6.stupně
a kořeny polynomu 6.stupně 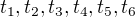
zjistíme, že platí  . To sice nelze považovat za důkaz ale naznačuje cestu.
. To sice nelze považovat za důkaz ale naznačuje cestu.
Podle věty o vztahu kořenů a koeficientů polynomu platí:
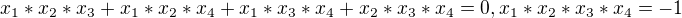
Máme tedy dokázat, že platí podobné vztahy pro polynom 6.stupně: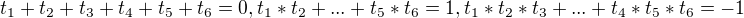

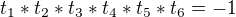 , když za
, když za 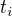 dosadíme příslušná
dosadíme příslušná 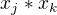 .
.
První a poslední vztah je evidentní. Další lze z rovnic pro 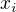 odvodit také,
odvodit také,
použijeme k tomu ještě vztahy  pro i=1,2,3,4 . Chce to jen
pro i=1,2,3,4 . Chce to jen
trpělivost, hodně papíru a nesplést se.
Zajímali by mne dvě věci: jak se na takovou zajímavou úlohu příjde a když toto je
jednodušší, jaká je ta složitější.
Offline
#3 09. 08. 2011 16:22 — Editoval xxMari (09. 08. 2011 16:23)
Re: Korene mnohočlenov (jednoduchšia úloha)
Offline
#5 13. 08. 2011 09:19 — Editoval musixx (13. 08. 2011 10:22)
Re: Korene mnohočlenov (jednoduchšia úloha)
To je celkem přímá úloha na použití elementárních symetrických polynomů.
Polynom více proměnných  nad tělesem
nad tělesem  je symetrický, jestliže když libovolně permutujeme "neznámé", tak se "nic nestane".
je symetrický, jestliže když libovolně permutujeme "neznámé", tak se "nic nestane".
Elementární symetrické polynomy v ![kopírovat do textarea $T[x_1,x_2,\dots,x_n]$](/mathtex/00/00cf42eb01def9682a71edd38ccb2038.gif) jsou
jsou
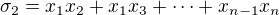
a tak dál až k 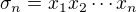 (dá se říct, že
(dá se říct, že  je součet všech možných součinů po
je součet všech možných součinů po  proměnných).
proměnných).
Poznámka: úplně přesně bychom měli psát 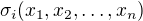 , ale držme se pro přehlednost jen toho
, ale držme se pro přehlednost jen toho  a
a  berme jako fixní.
berme jako fixní.
Vietovy vztahy pro všechny kořeny  libovolného polynomu jedné proměnné jsou proto až na střídající se znaménko vlastně přímo elementární symetrické polynomy v
libovolného polynomu jedné proměnné jsou proto až na střídající se znaménko vlastně přímo elementární symetrické polynomy v  .
.
No a když uvážíme množinu sestavenou z původních  , která je opět "symetrická" ve smyslu permutací jako výše, a hledáme-li polynom s těmito "novými" kořeny, pak Vietovy vztahy pro jeho kořeny budou opět symetrické polynomy proměnných
, která je opět "symetrická" ve smyslu permutací jako výše, a hledáme-li polynom s těmito "novými" kořeny, pak Vietovy vztahy pro jeho kořeny budou opět symetrické polynomy proměnných  .
.
Klíčová vlastnost symetrických polynomů n proměnných teď je, že libovolný takový polynom  se dá zapsat jako polynom
se dá zapsat jako polynom  a existuje v zásadě jednoduchý a přímočarý postup jak najít koeficienty polynomu
a existuje v zásadě jednoduchý a přímočarý postup jak najít koeficienty polynomu  .
.
--------------------
No a to je všechno. Někdo se tady ptal, jak takovou úlohu vymyslet. Odpovím: Není proto nijak těžké a ani početně dlouhé najít zcela obecně normovaný polynom šestého stupně, jehož kořeny jsou čísla 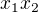 ,
, 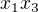 , až
, až 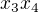 , kde
, kde  ,
,  ,
, 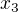 a
a 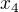 jsou kořeny polynomu
jsou kořeny polynomu 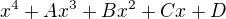 . Koeficienty budou nějaké výrazy obsahující čísla
. Koeficienty budou nějaké výrazy obsahující čísla  ,
,  ,
,  ,
,  a
a  . Pak jen stačí vybrat taková, aby jak polynom 4., tak polynom 6. stupně byly netriviální a vypadaly "hezky".
. Pak jen stačí vybrat taková, aby jak polynom 4., tak polynom 6. stupně byly netriviální a vypadaly "hezky".
Obdobně se dají řešit úlohy, kde hledaný polynom má mít třeba kořeny  (pak bude 4. stupně), nebo
(pak bude 4. stupně), nebo  (
(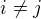 -- 6. stupeň), nebo třeba trochu absurdní
-- 6. stupeň), nebo třeba trochu absurdní  (nejmenší možný stupeň takového polynomu by pak pro
(nejmenší možný stupeň takového polynomu by pak pro  ,
,  ,
, 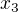 a
a 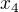 byl 12 -- to už by bylo dost otrockého počítání, ale může sloužit třeba jako námět někomu, kdo trochu umí programovat a chce se lehce procvičit) atd.
byl 12 -- to už by bylo dost otrockého počítání, ale může sloužit třeba jako námět někomu, kdo trochu umí programovat a chce se lehce procvičit) atd.
--------------------
Snad aspoň někdo bude mít radost z toho, že jsem se tady tak trochu víc rozepsal.
Offline
#6 14. 08. 2011 15:36
Re: Korene mnohočlenov (jednoduchšia úloha)
↑ musixx:
Viz mé řešení :-) Ostatně, celý můj postup byl v podstatě strojový, á la
Code:
SymmetricReduction[
SymmetricPolynomial[5, {a b, a c, a d, b c, b d, c d}], {a, b, c, d}]Offline


 su dva rozne korene
su dva rozne korene 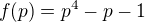 , potom
, potom 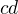 je koren
je koren 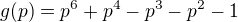 .
. .
.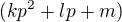 taky, ze plati
taky, ze plati  .Pouzitim Vietovych vztahov dostavame
.Pouzitim Vietovych vztahov dostavame 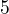 rovnic:
rovnic: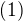

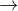

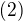
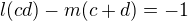

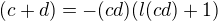
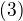

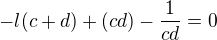 vyuzitim
vyuzitim 
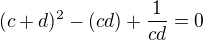

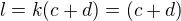

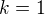
 a
a  , dosadenim do
, dosadenim do 

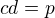 , teda
, teda 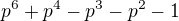 .
.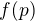 ,
, a tymi v zadani je
a tymi v zadani je  , potom plati:
, potom plati: 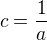 ,
,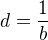
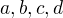 su nenulove staci dosadit do zadanych polynomov). Ukazali sme, ze
su nenulove staci dosadit do zadanych polynomov). Ukazali sme, ze 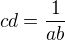
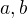 su korenmi
su korenmi 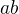 je korenom
je korenom 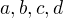 všechny čtyři kořeny
všechny čtyři kořeny  .
. . To ovšem má, jelikož
. To ovšem má, jelikož![kopírovat do textarea $(ab) \cdot (ac) \cdots (cd) &= (abcd)^3 = -1\\
[(ab)(ac)\cdots(bc)(bd)] + \dots + [(ac)(ad)\cdots(bd)(cd)] &= (abcd)^2(ab + ac + ad + bc + bd + cd) = 0\\
(ab)(ac)(ad)(bc) + \dots + (ad)(bc)(bd)(cd) &= abcd(a+b+c+d)(abc + abd + acd + bcd) - (abcd)^2 = -1\\
(ab)(ac)(ad) + \dots + (bc)(bd)(cd) &= abcd(a+b+c+d)^2 - 2abcd(ab + ac + ad + bc + bd + cd)\\ &{}+ (abc + abd + acd + bcd)^2 = -1\\
(ab)(ac) + (ab)(ad) + \dots + (bd)(cd) &= (a+b+c+d)(abc + abd + acd + bcd) - abcd = 1\\
(ab) + (ac) + \dots + (bd) &= 0$](/mathtex/d5/d51a718d61404168f23417b047b7ad2c.gif)