Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Užití diferenciálního počtu - příklady z geometrie (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 06. 2008 14:21
Užití diferenciálního počtu - příklady z geometrie
Offline
#2 17. 06. 2008 14:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užití diferenciálního počtu - příklady z geometrie
↑ Boykins:
Zdravim :-)
ke kazdemu prikladu musis sestavit funkci tak, aby byla funkci pouze jedne promenne (treba obvod odvozeny od jedne strany, kterou oznacis za x).
Dal tu funkci budes derivovat a budes hledat pro ktere x je derivace 0.
Ted zacni tak, ze pro kazde zadani navrchni neznamou a vzorce (geometrie) podle kterych to navrhujes pocitat.
Urcite to tady zkontrolujeme a navedeme, co dal.
OK?
Pro ostatni kolegy - dohlednete, prosim, tady na postupy (ja odchazim vyucovat rustinu :-). Zdravi a dekuje Jelena
Offline
#3 17. 06. 2008 14:53
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Užití diferenciálního počtu - příklady z geometrie
Příklad 4.43
Obsah pravoúhelníku je o stranách a,b
S = a*b (položíme rovno 1) můžeme protože je tento obsah znám.
Pak hledáme a,b takové, aby platilo 2(a+b) bylo minimální
a + b = minimum
Z výrazu a*b = 1 vyjádříme a
a = 1/b
dosadíme do a + b...... min
1/b +b ... min
Rovnici zderivujeme podle b a derivaci položíme rovnu nule
-1/b^2 +1 = 0
1/b^2 =1
b = 1
Dopočteme a
a = 1/b = 1/1 = 1
a = b
To znamená, že se jedná o čtverec (a = b)
Nikdo není dokonalý
Offline
#4 17. 06. 2008 19:59
Re: Užití diferenciálního počtu - příklady z geometrie
↑ jelena:
Tento postup znám, ale můj problém u těchto příkladů že jsem nenašel žádnou vhodnou kombinaci vzorců .. ostatní jsem tak nějak zvládnul, ale u těchto mám krizi :(
↑ Cheop:
Mockrát děkuji, v podstatě to byl podobný jako ten před ním, ale nemohl jsem se dopočítat, děkuji, tvůj postup byl i mnohem kratší a se správným výsledkem :-)
Offline
#5 17. 06. 2008 20:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užití diferenciálního počtu - příklady z geometrie
↑ Boykins:
Priklad 4.4 "uhlopricka" - predpokladame, ze mame obvod obdelniku P = 2(a+b),
a budeme povazovat za x,
b odvodime ze vzorce pro obvod
samotny obvod bude povazovan za konstantu
Delka uhlopricky se vypocita z Pythagorove vety, take pres a, b.
delka uhlopricky bude ta funkce, kterou tvorime. OK?
Offline
#7 17. 06. 2008 20:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užití diferenciálního počtu - příklady z geometrie
↑ Boykins:
mas to dobre, ted hledej, kde se to rovna 0 a to je pripade, kdyz citatel derivace je nulovy (jmenovatel nema vliv, ten se pouze zkontroluje na vysledek, zda ho neprevrati v 0 - ale to urcite nenastane)
Offline
#8 17. 06. 2008 21:02
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užití diferenciálního počtu - příklady z geometrie
obrazek k trojuhelniku:
asi budes volit variantu pres Pythagorovu vetu
http://forum.matweb.cz/upload/875-uziti.JPG
Offline
#9 17. 06. 2008 21:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užití diferenciálního počtu - příklady z geometrie
↑ Boykins:
http://euler.fd.cvut.cz/predmety/ml1/files/CV_ML1.pdf - tady jsou reseny valce str 72 a okolo a dost se toho resilo na tematech VS.
Offline
#11 17. 06. 2008 21:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užití diferenciálního počtu - příklady z geometrie
↑ Boykins:
:-)
ktery priklad jeste potrebujes naznacit?
Offline
#12 17. 06. 2008 22:21
Re: Užití diferenciálního počtu - příklady z geometrie
↑ jelena:
Nejspíše ještě ten 51 .. ale na to se podíwám zítra ráno, dnes už se mi začínají motat i ty nejzákladnější věci, které bych jinak neudělal špatně :-)
Mockrát vám děkuji za ochotu a velkou pomoc :-)
Offline
#13 17. 06. 2008 22:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užití diferenciálního počtu - příklady z geometrie
↑ Boykins:
OK :-)
Offline
#14 17. 06. 2008 23:30 — Editoval jelena (18. 06. 2008 01:10)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Užití diferenciálního počtu - příklady z geometrie
↑ Boykins:
Mela bych pro jistotu varovat pred kvalitou provedeni :-)
http://forum.matweb.cz/upload/790-hranol.JPG
zapornou hodnotu a nebereme :-)
Offline
#15 18. 06. 2008 08:39
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Užití diferenciálního počtu - příklady z geometrie
Příklad 4.45


Rovnici derivujeme podle b a derivaci položíme rovno nule
Stačí když zderivuje výraz pod odmocninou.
Za b dosadíme do rovnice  a vyjádříme druhý rozměr
a vyjádříme druhý rozměr
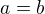 jedná se o čtverec
jedná se o čtverec
Nikdo není dokonalý
Offline
#16 18. 06. 2008 09:08 — Editoval Cheop (18. 06. 2008 09:11)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Užití diferenciálního počtu - příklady z geometrie
Příklad 4.53 - povrch válce
- povrch válce - objem válce maximum
- objem válce maximum
Z rovnice pro povrch vyjádříme výšku v dosadíme do rovnice pro výpočet objemu
dosadíme do rovnice pro výpočet objemu
Po úpravě dostaneme (nebudu tady tu úpravu rozepisovat, protože psaní v tomto programu mi dělá ještě potíže) derivujeme podle r a dostaneme:
derivujeme podle r a dostaneme: výsledek dosadíme do rovnice:
výsledek dosadíme do rovnice: a určíme výšku válce
a určíme výšku válce
Po malých úpravách dospějeme k výsledku:
 - průměr válce
- průměr válce
Průměr válce je stejný jako jeho výška
(Myslím, že se tomu říká rovnostranný válec - nevím jsem jen zemědělec)
PS podobný postup se použije i u příkladu 4.54
Nikdo není dokonalý
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Užití diferenciálního počtu - příklady z geometrie (TOTO TÉMA JE VYŘEŠENÉ)

