Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » konverg FOTO doplnenie postupu (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 06. 2011 11:32 — Editoval vysoka (20. 06. 2011 11:37)
konverg FOTO doplnenie postupu
zdravicko pondelok byva modry a tak makame az sa nam z kecky pari :)
zatial v pohode ... ? ako upravy tak aj spravne kriterium ? :)
hmmmmmm.........
http://www.wolframalpha.com/input/?i=li … %2F%283%29
Offline
- (téma jako vyřešené označil(a) vysoka)
#4 24. 08. 2011 12:02 — Editoval OiBobik (24. 08. 2011 12:06)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: konverg FOTO doplnenie postupu
↑ vysoka:
Zdravím,
provedl bych odhad 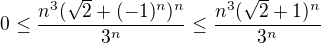 a ukázal, že
a ukázal, že 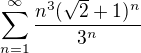 konverguje - to lze snadno podílovým nebo odmocninovým kritériem.
konverguje - to lze snadno podílovým nebo odmocninovým kritériem.
(pozn: ta limita v tvém postupu totiž neexistuje, tedy ten odhad je nutný)
EDIT: jubilejní 500. příspěvek, tak snad se nepletu, to by byla škoda. : ))
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 24. 08. 2011 12:50 — Editoval vysoka (24. 08. 2011 12:55)
#6 24. 08. 2011 13:50
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: konverg FOTO doplnenie postupu
↑ vysoka:
jj, je to tak.
jen pro doplnění: Tímhle jsme dokázali to, že posloupnost částečných součtů 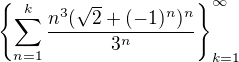 je shora omezená (neboť jsme našli konvergentní majorantu) a vzhledem k nezápornosti členů
je shora omezená (neboť jsme našli konvergentní majorantu) a vzhledem k nezápornosti členů 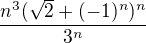 víme, že je i monotónní(neklesající) - tedy musí mít reálnou limitu a tím pádem vyšetřovaná suma konečný součet.
víme, že je i monotónní(neklesající) - tedy musí mít reálnou limitu a tím pádem vyšetřovaná suma konečný součet.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » konverg FOTO doplnenie postupu (TOTO TÉMA JE VYŘEŠENÉ)
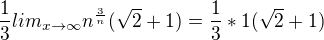 / q<1 --> konverguje :)
/ q<1 --> konverguje :)