Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » diferencialni rovnice 3-radu (TOTO TÉMA JE VYŘEŠENÉ)
#5 25. 08. 2011 06:27 — Editoval vysoka (25. 08. 2011 07:21)
Re: diferencialni rovnice 3-radu
6,s poc. podmienkou ↑ Olin: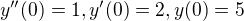 ?
?
...
môže byť 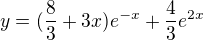 ?
?
poradte prosim ako si tie derivacie moyem skontrolovat vo wolfram ... http://www.wolframalpha.com/input/?i=de … **%282x%29 ? "hracky s vyjadrovanim som zvladol podla spatnej skusky celkom dobre" :)
Offline
#6 25. 08. 2011 12:14
Re: diferencialni rovnice 3-radu
W|A patrně nemá rád zápisy jako C_1, radši použij samostatná písmen A, B, C.
Jinak 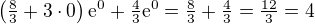 , takže je to zřejmě špatně.
, takže je to zřejmě špatně.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » diferencialni rovnice 3-radu (TOTO TÉMA JE VYŘEŠENÉ)
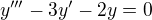
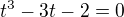 ?
?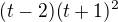 ?
?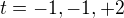 ?
?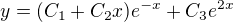 ?
?