Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Fyzika
- » Kyvadlo - delka kyvadel neznama jen pocty kmitu a jejich rozdil delek.
#1 25. 08. 2011 13:12 — Editoval dorfik (25. 08. 2011 13:17)
Kyvadlo - delka kyvadel neznama jen pocty kmitu a jejich rozdil delek.
Opět a snad naposledy vás prosím, jestli by mi někdo nemohl objasnit výpočet tohoto příkladu. Zítra dělám reparát, včera jsem byl i na doučování za spolužačkou, ale i ta nevěděla, jak se tenhle typ příkladu řeší.
Za tutéž dobu vykoná jedno kyvadlo 50 kmitů a druhé 30 kmitů. Určete délku kyvadel, jestliže rozdíl jejich délek je 32 cm.
To = 2*pí*sqrt(m/k) k=mg/delta l
Předem moc děkuji.
Offline
#2 25. 08. 2011 13:22
Re: Kyvadlo - delka kyvadel neznama jen pocty kmitu a jejich rozdil delek.
Vzorec pro délku kmitu kyvadla je: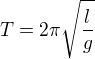
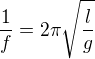
toto bude tedy jedna rovnice a druhá bude:
Možná je to špatná úvaha, ale momentálně mě napadlo tohle. Akorát mi dělá starosti ta frekvence, protože tam není udáno, že je to za sekundu - kdyby ta určitá doba byla sekunda, bylo by to takto... třeba někdo s kolegů vymyslí něco lepšího.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#4 25. 08. 2011 13:27
Re: Kyvadlo - delka kyvadel neznama jen pocty kmitu a jejich rozdil delek.
No, jsou to prostě dvě rovnice o dvou neznámých (frekvenci a délce).  jak otakové je délka kratšího kyvadla, délka delšího kyvadla pak bude
jak otakové je délka kratšího kyvadla, délka delšího kyvadla pak bude  .
.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#6 25. 08. 2011 13:41
Re: Kyvadlo - delka kyvadel neznama jen pocty kmitu a jejich rozdil delek.
Když píšeš v TeXu řecká písmena, musíš před ně dát \, poté se zobrazí správně. :-)
Nejsem si však jist, proč by měla být převrácená hodnota u dvou pí...
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#7 25. 08. 2011 13:44
Re: Kyvadlo - delka kyvadel neznama jen pocty kmitu a jejich rozdil delek.
Ahojte a posielam z iného súdku...
http://cs.wikipedia.org/wiki/Matematick%C3%A9_kyvadlo
T=doba periody=doba 1kmitu, a ešte jeden vzťah t=n.T koľko času uplynie, po n kmitoch.
Prvé kyv. t=50.2pí.sqrt(l1/g)
Druhé kyv. t=30.2pí.sqrt(l2/g)
t=t
50.2pí.sqrt(l1/g)=30.2pí.sqrt(l2/g)......jedna rovnica
l2-l1=0,32 alebo l1-l2=0,32......druhá rovnica
Offline
#8 25. 08. 2011 13:44 — Editoval found (25. 08. 2011 13:51)
Re: Kyvadlo - delka kyvadel neznama jen pocty kmitu a jejich rozdil delek.
Myslím, že už vím, jak by ty rovnice měly vypadat:


Frekvence je počet kmitů za určitý čas, proto je to n/T0 - počet kmitů prvního kyvadla
- počet kmitů prvního kyvadla - počet kmitů druhého kyvadla
- počet kmitů druhého kyvadla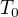 - doba, po kterou se kyvadlo pohybuje
- doba, po kterou se kyvadlo pohybuje - délka prvního kyvadla
- délka prvního kyvadla - délka druhého kyvadla
- délka druhého kyvadla
počítáš  a můžeš i
a můžeš i 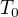
Takže kolega ↑ pietro: to měl hned lépe, jak teď tak koukám, nestihl jsem to napsat dostatečně rychle. :-)
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#11 25. 08. 2011 14:01
Re: Kyvadlo - delka kyvadel neznama jen pocty kmitu a jejich rozdil delek.
Ahojte, už len doplním...
http://www.wolframalpha.com/input/?i=50 … &cdf=1
Offline
#12 25. 08. 2011 14:58 — Editoval Rumburak (25. 08. 2011 15:05)
Re: Kyvadlo - delka kyvadel neznama jen pocty kmitu a jejich rozdil delek.
Offline
Stránky: 1
- Hlavní strana
- » Fyzika
- » Kyvadlo - delka kyvadel neznama jen pocty kmitu a jejich rozdil delek.

 ,
,  ,
, 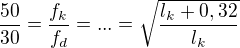
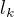 .
.