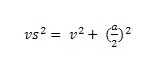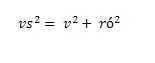Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 08. 2011 14:47
výška stěny v jehlanu
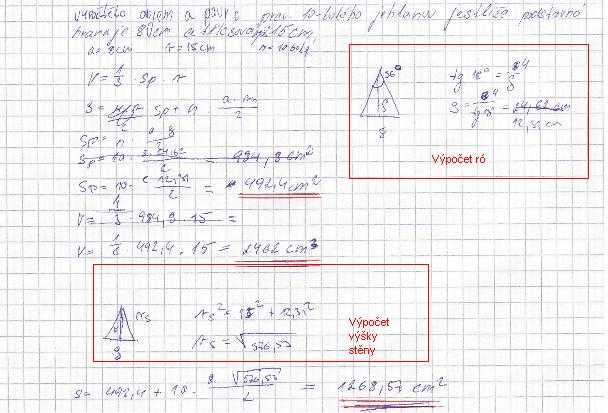
Zdravim , potřeboval bych jen poradit jaký je správnej vzoreček pro vypočítání výšky stěny v jehlanu. Mám tu dva vzorečky
1 . 
2. 
kdyžtak tady mám vypočítaný příklad .. ale nejsem si jistej jestli je správně, protože sem někde viděl že se výška stěny počítá -> 1.
děkuju za výpomoc
Offline
- (téma jako vyřešené označil(a) janca361)
#2 25. 08. 2011 15:43 — Editoval Rumburak (26. 08. 2011 10:49)
Re: výška stěny v jehlanu
↑ Koucis:
Záleží na druhu jehlanu.
Máme-li pravidelný n-boký jehlan, který má tělesovou výšku 
a do jehož podstavy (což je pravidelný n-úhelník) je vepsána kružnice
o poloměru 
, potom platí druhý vzorec (protože bod dotyku oné kružnice se stranou podstavy je totožný s patou výšky příslušné stěny
a zároveň střed této kružnice je patou tělesové výšky - zmíněné dva body spolu s vrcholem kužele tvoří pravoúhlý trojúhelník s přeponou 
a odvěsnami 
, proto vzorec vypadá právě takto - viz Pythahorova věta).
Máme-li pravidelný čtyřboký jehlan, který má tělesovou výšku a jehož podstava (což je čtverec) má stranu délky 
, potom je správný
i první vzorec (protože v tomto případě 
).
U nepravidelných jehlanů může mít každá strana jinou výšku, takže jednotný vzorec neexistuje.
Offline
#3 25. 08. 2011 15:54 — Editoval Koucis (25. 08. 2011 15:57)
Re: výška stěny v jehlanu
↑ Rumburak:takže se spíše používá druhý vzorec? Může se druhý vzorec používat i u čtvercové či obdélníkové podstavy nebo se to nepoužívá protože u čtvercové podstavy nemusíme počítat ró? děkuji
Offline
#4 25. 08. 2011 16:19 — Editoval Rumburak (26. 08. 2011 10:54)
Re: výška stěny v jehlanu
↑ Koucis:
Pokud jde o mne, já nepoužívám žádný vzorec, prostě si ujasním, co je zadáno, a snažím se najít tam nějaký vztah k výšce některé stěny.
U čtvercové podstavy , pokud jde o pravidelný jehlan (pata tělesové výšky padne do středu podstavy), jsou správné oba vzorce, jak už jsem
napsal v předchozím příspěvku.
U obdélníkové podstavy, pokud její střed (průsečík úhlopříček) je zároveň patou tělesové výšky spuštěné s hlavního vrcholu, platí vzorce
obdobné tomu prvnímu s tím, že u dvou sousedních stěn se jejich výšky budou lišit v závislosti na tom, jak se u podstavy budou lišit dvě
sousední strany, jejichž délky by se do vzorce dosazovaly. K lepšímu pochopení si nakresli obrázek a zkus tam hledat pravoúhlé trojúhelníky,
jejichž přeponami jsou výšky stěn.
Offline