Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 04. 09. 2011 22:56
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Mám další problém, nechápu, co se stalo té jedničce.
matematik amathér
Offline
#28 04. 09. 2011 23:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Zlomky
Zdravím,
1) pořád vkládáš příspěvky do již vyřešeného tématu (pokud to navazuje, tak to téma prosím "odznač" v 1. příspěvku), jenže
2) nenavazuje příliš - protože tento dotaz už tady byl Tobě odpovězen, tedy pokračuj prosím v původním tématu.
Přečti si, prosím, pravidla mat. fóra (kolegovi Oxyd se omlouvám za vstup do výkladu). Děkuji.
Offline
#29 04. 09. 2011 23:14
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Omlouvám se, zapomněl jsem, že jsem už řešil tenhle příklad. V/Vo - 1 bych uměl řešit do fáse V/Vo-1/1, dále tomu nerozumím.
matematik amathér
Offline
#30 04. 09. 2011 23:25
Re: Zlomky
První krok máš dobře, 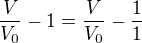 . Pro odečtení dvou zlomků potřebuju, aby měli oba stejné jmenovatele -- tady můžu rozšířit zlomek 1/1 číslem
. Pro odečtení dvou zlomků potřebuju, aby měli oba stejné jmenovatele -- tady můžu rozšířit zlomek 1/1 číslem 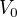 . Rozšířit zlomek číslem znamená vynásobit tím číslem čitatele i jmenovatele. Tady násobím číslem
. Rozšířit zlomek číslem znamená vynásobit tím číslem čitatele i jmenovatele. Tady násobím číslem 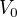 , abych 1/1 dostal do tvaru něco / V_0. Konkrétně ho dostanu do tvaru
, abych 1/1 dostal do tvaru něco / V_0. Konkrétně ho dostanu do tvaru 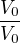 . Takže z toho teďka mám
. Takže z toho teďka mám 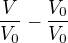 . Když už mám v obou zlomcích stejné jmenovatele, tak je můžu odečíst tak, že vyrobím zlomek, ve kterém je v čitateli rozdíl čitatelů původních dvou zlomků a ve jmenovateli je ten společný jmenovatel. V tomhle případě:
. Když už mám v obou zlomcích stejné jmenovatele, tak je můžu odečíst tak, že vyrobím zlomek, ve kterém je v čitateli rozdíl čitatelů původních dvou zlomků a ve jmenovateli je ten společný jmenovatel. V tomhle případě: 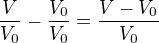 .
.
Což je přesně to, co se stalo té jedničce.
Více o operacích se zlomky si můžeš najít tady. Ostatně, celý Matweb (ke kterému tohle fórum patří) by ti mohl posloužit jako dobrý zdroj pro dohánění matiky.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#31 05. 09. 2011 00:11
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Matweb, alespoň sekci zlomky a pár dalších, jsem si prošel, ale věci z tohohle threadu jsem tam nenašel. Co do čísel si se zlomky jakžtakž poradím, ale když se tam přidají proměnné, dělá mi to problémy. Každopádně díky, už to taky chápu.
matematik amathér
Offline
#32 05. 09. 2011 00:18 — Editoval matematik123 (05. 09. 2011 00:19)
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Co mi ale není jasné, je tenhle příklad (1. krok):
mě osobně vyšlo aá=faá+faá
matematik amathér
Offline
#33 05. 09. 2011 00:23
Re: Zlomky
Levou stranu si vykrátil dobře -- f se tam škrtlo. Na pravé musíš také krátit (o to ostatně jde -- vykrátit ty zlomky tak, že už tam nebudou) -- pravá strana po vynásobení je 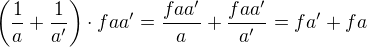 .
.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#34 05. 09. 2011 00:33
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
A ta spodni cast zlomku se vubec nenasobi, ze?
matematik amathér
Offline
#35 05. 09. 2011 00:44
Re: Zlomky
↑ matematik123:
Když násobíš zlomek obyčejným nezlomkovým číslem, tak násobíš jenom čitatele, ano.
Obecně, zlomky se násobí takhle: 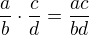 . Když chceš například násobit
. Když chceš například násobit 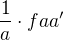 , tak z druhého činitele nejdřív uděláš zlomek a pak to vynásobíš jako dva zlomky --
, tak z druhého činitele nejdřív uděláš zlomek a pak to vynásobíš jako dva zlomky -- 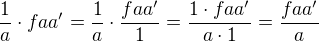 .
.
Proto se při násobení „nezlomkem“ násobí jenom ten čitatel -- jmenovatel se akorát přenásobí jedničkou, takže se s ním vůbec nic nestane.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#36 05. 09. 2011 10:01
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Aha, přesně takhle jsem to dělal jen jsem to špatně pokrátil. Díky za radu.
matematik amathér
Offline
#37 05. 09. 2011 10:18
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Tak mám další problém, druhý příklad jsem vyřešil bez problémů, ale nechápu co udělali s tím prvním. Konkrétně v druhém kroku. Já odstranil zlomek jako v druhém příkladě, vytknul R a vyšlo mi to stejně, jako v níže uvedeném příkladu. Přesto bych ale rád věděl, co s ním udělali oni. 
matematik amathér
Offline
#38 05. 09. 2011 10:49
Re: Zlomky
Ahoj u celkovýho odporu první krok udělali ten, že na pravé straně dali zlomek na společnýho jmenovatele. Potom 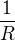 je vlastně převrácená hodnota zlomku. Vlastně vše co je
je vlastně převrácená hodnota zlomku. Vlastně vše co je 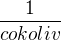 se jen u těchto případů prohodí čitatel s jmenovatelem na obou stranách rovnice, aby jsme měli v tomto případě čisté R a ne
se jen u těchto případů prohodí čitatel s jmenovatelem na obou stranách rovnice, aby jsme měli v tomto případě čisté R a ne  . Je jednosušší a rachlejší si pamatovat toto pravidlo něž sdlouhavě upravovat rovnici jde hlavně o to si ulehčit práci a ztratit co nejmíň času při počítání s úpravou rovnic.
. Je jednosušší a rachlejší si pamatovat toto pravidlo něž sdlouhavě upravovat rovnici jde hlavně o to si ulehčit práci a ztratit co nejmíň času při počítání s úpravou rovnic.
Offline
#40 05. 09. 2011 11:29 — Editoval Rumburak (05. 09. 2011 11:30)
Re: Zlomky
↑ matematik123:
Ještě mírně jinak.
Upravujeme tedy rovnici
(1)  .
.
Nejprve sečteme zlomky na pravé straně : ,
,
tím rovnice (1) dostane tvar
(2)  .
.
Tuto rovnici (tedy každou její stranu) vynásobíme výrazem 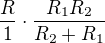 , vznikne
, vznikne
 .
.
neboli
 ,
,
po vykrácení zlomků a vynechání zbytečných jedniček zůstane
 .
.
Šlo by i provádět to postupně po menších krůčcích - vyzkoušej.
Offline
#41 05. 09. 2011 11:33 — Editoval Cheop (05. 09. 2011 13:37)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Zlomky
↑ matematik123: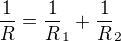
První krok pravou stranu rovnice dáme na společného jmenovatele tj: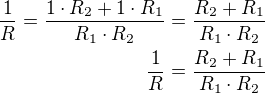
Ve druhém kroku čitatel levé strany vynásobíme součinem R_1 . R_2 a čitatel pravé strany vynásobíme R tedy: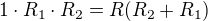
Teď už jenom z této rovnice vyjádříme R tj: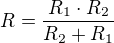
Nikdo není dokonalý
Offline
#42 11. 09. 2011 20:24
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Mám dalším problém - krácení zlomků. Nechápu, jak je mohu krátit když dělím/násobím a sčítám/odčítám. Nemůžete mi prosím pomoci?
matematik amathér
Offline
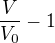 ?
?