Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 09. 2011 18:47
- Jan Jícha

- Veterán

- Místo: Plzeň/Mnichov
- Příspěvky: 1801
- Škola: ZČU - FST - KMM
- Pozice: Safety Engineer
- Reputace: 74
- Web
Tečna
Ahoj, řešit tento příklad přes soustavu 2 rovnic o 2 neznámých s jedním parametrem se mi nechtělo.
Jak to půjde řešit jinak?
Napište tečnu ke křivce z bodu
Respektive jak si upravit tu elipsu, aby to šlo derivovat:)
Offline
#2 12. 09. 2011 19:29
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Tečna
Tenhle postup mi fungoval u kružnice, tak snad pofičí i u elipsy...
Vyjádři si y (nepříjemné :-)) Bude to chtít řešit parametricky kvadrovnici, ale pro tebe určitě žádný problém ;)
Wolfram
Urči, který "oblouk" je horní a který spodní.
Vyber správný.
Derivuj...atd
Offline
#5 12. 09. 2011 19:44
- Jan Jícha

- Veterán

- Místo: Plzeň/Mnichov
- Příspěvky: 1801
- Škola: ZČU - FST - KMM
- Pozice: Safety Engineer
- Reputace: 74
- Web
Re: Tečna
↑ Hanis:↑ o.neill:
Dík, já jsem to myslel bez vyjadřování jestli se to nedá nějak vhodně upravit:)
Jinak Dano, ten bod neleží na té elipse.
Offline
#7 12. 09. 2011 21:49
#8 13. 09. 2011 09:22 — Editoval xxMari (13. 09. 2011 10:49)
Re: Tečna
Uvažujme 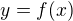 , potom
, potom 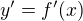 .
.
Derivovaním (podľa x) máme 
 ,
,
pre  , teda
, teda 
Pozn.: 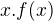 derivujeme ako "súčin" t.j
derivujeme ako "súčin" t.j 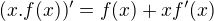 a
a  ,
,
kde  predstavuje nejaký "výraz" premennej x (konkrétne ten z príspevku ↑ o.neill:).
predstavuje nejaký "výraz" premennej x (konkrétne ten z príspevku ↑ o.neill:).
Pre rovnicu dotyčnice ku funkcii  v bode
v bode  platí :
platí :  ,
,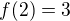 - dopočítaním kvadratickej rovnice (zo zadania) pre
- dopočítaním kvadratickej rovnice (zo zadania) pre  a uvážením
a uvážením  .
.
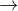

(Pozn.:tento postup využíva aj niečo z VŠ matematiky)
Offline
#9 13. 09. 2011 10:38
Re: Tečna
↑ o.neill:
Nie je jednoduchšie proste doplniť do rovnice tej elipsy namiesto  ,
,  keďže x-ovú súradnicu bodu vieme, a z toho riešiť normálnu kvadratickú rovnicu kde výjdu obe
keďže x-ovú súradnicu bodu vieme, a z toho riešiť normálnu kvadratickú rovnicu kde výjdu obe  ? A nemusím potom vyjadrovať komplet celé
? A nemusím potom vyjadrovať komplet celé  skrz parametrickú rovnicu.
skrz parametrickú rovnicu.
Offline
#10 13. 09. 2011 10:49 — Editoval Cheop (13. 09. 2011 10:52)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Tečna
↑ nehalem:
On ↑ o.neill: vyjádřil y z té rovnice elipsy proto, aby ho mohl derivovat a určit tak
směrnici "k" tečny k té elipse, z rovnice:
Nikdo není dokonalý
Offline
#12 13. 09. 2011 10:54
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Tečna
↑ nehalem:
To se mýlíš jde to i jinak.
Pokud budeš mít zájem mohu sem jiný postup řešení
bez derivací napsat.
Nikdo není dokonalý
Offline
#14 13. 09. 2011 10:56
#15 19. 09. 2011 00:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Tečna
Zdravím, přidám řešení od kolegy Zdeňka, děkuji :-)
Lze považovat za vyřešené?
Offline

